【题解】[SCOI2007] 最大土地面积 旋转卡壳 BZOJ – 1069

题目链接

似乎思路还是挺显然的

最大的四边形的顶点一定都是在凸包上的

然后发现 $n \leq 2000$，因此考虑 $n ^ 2$（或者 $n ^ 2 log _ 2 n$）

于是 $n ^ 2$枚举四边形的一条对角线，四边形被这个对角线分为上下两个三角形

这时候就要找到上半平面中距离这条对角线最远的点和下半平面中距离对角线最远的点

这个就用两根平行与对角线的直线去旋转卡壳找到

如图所示：

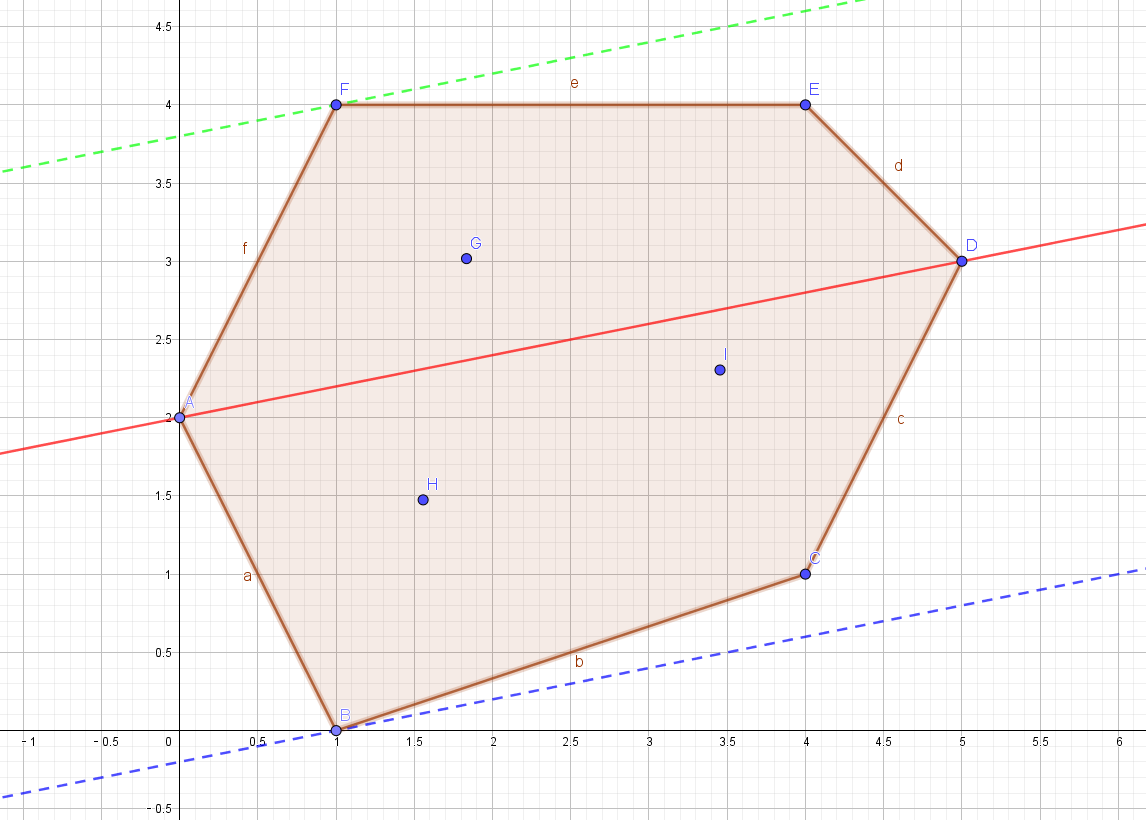
（红色是对角线，蓝色是下切线，绿色是上切线）

如果你 lower_bound 找切点复杂度就是 $O(n ^ 2 log _ 2 n)$，实测洛谷跑得过

但其实在凸包里按顺序枚举点对时对角线的斜率是单调的，因此 two-point 扫一遍即可，复杂度 $O(n ^ 2)$

（然而我这份代码依然又长又慢，主要是凸包我是用射线维护的，然后维护每条射线的极角这样。。。然后又是 STL 就很慢了）

#include <bits/stdc++.h>

#define NS (2005)
#define eps (1e-10)
#define dCmp(a, b) (fabs((a) - (b)) < eps)

using namespace std;

const double PI = acos(-1);

struct vec // 向量 &点
{
    double x, y;
    vec() {x = 0, y = 0;}
    vec(double a, double b) {x = a, y = b;}
    vec operator - (const vec oth) const {return vec(x - oth.x, y - oth.y);}
    double crs(const vec oth) {return x * oth.y - y * oth.x;} // 叉积
} P[NS];

struct ray // 射线
{
    vec p, q; double angle; // 极角，范围 [0, 2 * PI]
    ray() {p = vec(0, 0), q = vec(0, 0), angle = 0;}
    ray(vec a, vec b)
    {
        p = a, q = b;
        angle = atan2(q.y, q.x);
        if (angle < 0) angle += PI * 2;
    }
    bool operator < (ray oth)
    {
        if (dCmp(angle, oth.angle)) return 0;
        return angle < oth.angle;
    }
};

int n;

bool dlCmp(const vec a, const vec b)
{
    if (dCmp(a.y, b.y)) return a.x < b.x;
    return a.y < b.y;
}

bool anCmp(const vec a, const vec b) // 以 P[1]（最下方最左边的点）为原点极角排序
{
    return atan2(a.y - P[1].y, a.x - P[1].x)
        < atan2(b.y - P[1].y, b.x - P[1].x); // 实际上 atan2 很慢，大概有 10 倍常数
}

typedef vector<ray>::iterator itr;
vector<ray> poly;

void getPoly()
{
    sort(P + 1, P + 1 + n, dlCmp), sort(P + 2, P + 1 + n, anCmp); // 最下方最左边的点一定在凸包上
    poly.push_back(ray(P[1], P[2] - P[1]));
    for (int i = 3; i <= n; i += 1)
    {
        ray tmp(P[i - 1], P[i] - P[i - 1]);
        while (!poly.empty() && !(poly[poly.size() - 1] < tmp))
        {
            tmp = ray(poly[poly.size() - 1].p, P[i] - poly[poly.size() - 1].p);
            poly.pop_back();
        }
        poly.push_back(tmp);
    }
    ray tmp(P[n], P[1] - P[n]);
    while (!poly.empty() && !(poly[poly.size() - 1] < tmp))
    {
        tmp = ray(poly[poly.size() - 1].p, P[1] - poly[poly.size() - 1].p);
        poly.pop_back();
    }
    poly.push_back(tmp);
}

int main(int argc, char const* argv[])
{
    scanf("%d", &n);
    if (n <= 2) puts("Error!"), exit(0);
    for (int i = 1; i <= n; i += 1) scanf("%lf%lf", &P[i].x, &P[i].y);
    getPoly();
    double ans = 0;
    for (int i = 0; i < poly.size(); i += 1)
    {
        itr d = poly.begin(), u = poly.begin(); // d -> 下切线（r1 顺时针方向）u -> 上切线
        for (int j = i + 1; j < poly.size(); j += 1)
        {
            ray r1(poly[i].p, poly[j].p - poly[i].p);
            ray r2(poly[j].p, poly[i].p - poly[j].p);
            while (d != poly.end() && *d < r1) d++;
            while (u != poly.end() && *u < r2) u++;
            if (d == poly.end()) d--;
            if (u == poly.end()) u--;
            vec t1 = d->p - poly[i].p, t2 = poly[j].p - poly[i].p;
            double res = t1.crs(t2);
            t1 = u->p - poly[i].p;
            res += t2.crs(t1);
            ans = max(ans, res * 0.5);
        }
    }
    printf("%.3f\n", ans);
    return 0;
}