吐槽
这什么鬼定理,命名者太自恋了吧
什么是 BEST 定理?
让我们先看看百度搜出来的前几篇大佬文怎么说
大佬文 1:

直接丢俩链接跑路,真爽
大佬文 2:

为啥是欧拉路径???说好的欧拉回路呢?BEST 定理诚不我欺???
而且 $ec(G)$是回路个数啊,回路是没有起点的啊,如果是以 $s$为起点是 $ec _ s(G)$啊。
而且而且为什么 $v \not = s$?就算是 $ec _ s(G)$也应该算上 $(deg[s] – 1)!$啊,不然答案会错的啊
要么就是把式子中的 $deg[s]$改成 $deg[s]!$才对啊
写啥呢大爷,自己写的式子计算过吗?闭着眼睛写的?
大佬文 3:
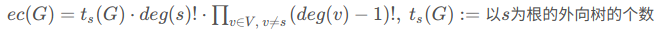
和第 2 位大佬一个问题
大佬文 4:

怎么和第 3 位大佬一模一样啊,心灵感应啊
大佬文 5:
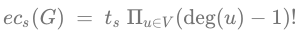
明明写的是不计起点的 $ec(G)$,等号左边却写着 $ec _ s(G)$
要我说他们要么就别写,写成这样居然百度排这么前面,毒瘤吗?!
4 个人,三种不同的公式
人才啊,都™是人才
既然要写就写好点,要么就别写,拿出来恶心人干嘛
不过说起来别人也没逼着我看他写的,他写得一塌糊涂是他的自由
但是百度就是真的制杖了啊,没点技术的吗?粗制滥造的文章,完全不检查的公式与文字都能排那么前面,贴俩链接就能排第一
那些优质的文章何处去呢?
题解
这是 BEST 定理裸题
BEST 定理是什么?
$\operatorname{ec}(G) = t _ w(G) \prod _ {v\in V} \bigl(\deg(v)-1\bigr)!$
这要是有错我直播跳楼!倒挂跳楼!
我就不知道了,这些博主不晓得去维基百科搜一下吗???
这么简单的公式搞得云里雾里的
其中 $ec(G)$表示有向图 $G$的欧拉回路个数!
比如如下这个图:
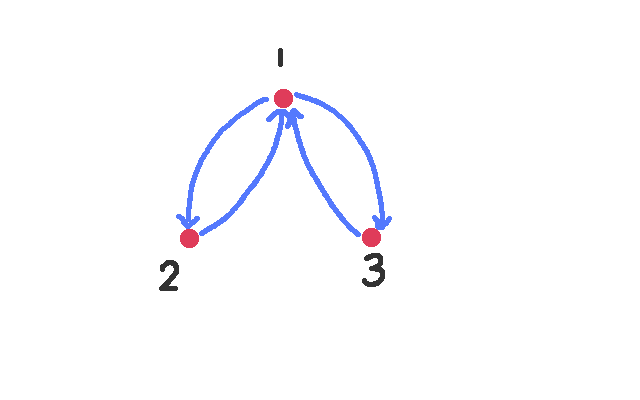
欧拉回路只有 $1$个!
因为环只有一个!与你先遍历 $2$还是先遍历 $3$无关!
就像你画一个圆,你从圆底部开始画和从顶部开始画有区别吗?你会把这两个圆称作 “不同的圆” 吗?
网上那些博主连这个都分不清楚还写啊写啊写,真的是绝了
公式中的 $deg(v)$,则表示 $v$的度数,这个度数可以为入度也可以为出度,因为有向图存在欧拉回路的充要条件是
任意一个点的入度和出度都相同
然后 $t _ w(G)$表示以 $w$为根的外向树个数,这个用矩阵树定理算就行了,基尔霍夫矩阵=度数矩阵-邻接矩阵
度数矩阵 $D[i][i]=deg(i)$
邻接矩阵。。。就是邻接矩阵
至于这一题求的是 “从 1 出发遍历点的顺序不同的方案数”(即图中先去 2 和先去 3 是不同方案),只要把环的个数乘以 $deg(1)$就行了,因为每个环都有 $deg(1)$种进入环的方法
代码:
#include <bits/stdc++.h>
#define NS (105)
#define MOD (1000003)
#define pls(a, b) ((a) + (b) < MOD ? (a) + (b) : (a) + (b) - MOD)
#define mns(a, b) ((a) - (b) < 0 ? (a) - (b) + MOD : (a) - (b))
#define mul(a, b) (1ll * (a) * (b) % MOD)
using namespace std;
template<typename _Tp> inline void IN(_Tp& dig)
{
char c; bool flag = 0; dig = 0;
while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
if (flag) dig = -dig;
}
int n, D[NS][NS], deg[NS], ideg[NS], fac[200005];
int det()
{
int res = 1;
for (int i = 1; i < n; i += 1)
{
for (int j = i + 1; j < n; j += 1)
while (D[j][i])
{
int tmp = D[i][i] / D[j][i];
for (int k = i; k < n; k += 1)
D[i][k] = mns(D[i][k], mul(tmp, D[j][k]));
swap(D[i], D[j]), res = mns(0, res);
}
res = mul(res, D[i][i]);
}
return res;
}
int main(int argc, char const* argv[])
{
fac[0] = 1;
for (int i = 1; i <= 200000; i += 1) fac[i] = mul(fac[i - 1], i);
while(IN(n), n)
{
memset(D, 0, sizeof(D)), memset(ideg, 0, sizeof(ideg));
for (int i = 1; i <= n; i += 1)
{
IN(deg[i]);
for (int j = 1, k; j <= deg[i]; j += 1)
{
IN(k), ideg[k]++;
D[i][k] = mns(D[i][k], 1), D[k][k] = pls(D[k][k], 1);
}
}
if (n == 1) {printf("%d\n", fac[deg[1]]); continue;}
for (int i = 1; i <= n; i += 1)
if (deg[i] != ideg[i]) {puts("0"); continue;}
for (int i = 1; i < n; i += 1)
{
swap(D[i], D[i + 1]);
for (int j = 1; j <= n; j += 1) D[i][j] = D[i][j + 1];
}
int t = mul(det(), deg[1]);
for (int i = 1; i <= n; i += 1) t = mul(t, fac[deg[i] - 1]);
printf("%d\n", t);
}
return 0;
}
3 条评论
ShuYuMo · 2021年3月29日 7:43 上午
写的很好啊 /QAQAQAQ
Remmina · 2021年3月29日 2:48 下午
看着自己以前写的感觉自己好幼稚啊 23333
ShuYuMo · 2021年3月29日 2:50 下午
幼稚归幼稚 但是比其他的博客确实会好一些 /CY 其他的没有讲清楚等价类的划分规则是什么 就很迷惑…