1. 是什么
似乎很多地方直接管它叫 Pollard rho 算法
又名泼辣的肉算法
用于对 $n$进行质因数分解
根据生日悖论,复杂度大约是 $O(n ^ \frac 1 4)$的(算法导论中写的复杂度更准确,不过无伤大雅)
2. 算法
假设我们要分解 $n$,那么首先 Miller-Rabin 判断其是否是素数,如果是的话直接返回 $n$
(Miller-Rabin 可以看我的上一篇文章:戳我 QAQ)
否则只要找到一个 $k$,使得 $gcd(n, k) \not = 1$
设 $gcd(n, k) = d$
我们只要继续分解 $\frac n d$和 $d$即可
为什么要这样呢?因为虽然直接找到 $d$的概率比较小,但是找到 $d$的一个倍数的概率是直接找到 $d$的若干倍,同时 $d$有可能有很多个,因此概率就不小了
于是我们搞一个数组 $x$,令 $x _ 0 = 2$,然后 $x _ i = x _ {i – 1} ^ 2 + c(i > 0)$
其中 $x _ 0 = 2$其实也可以随机设一个初始值,然后 $c$是一个常数,在生成 $x$数组前随机一个就行了
对于 $x$中相邻的两项 $x _ i$与 $x _ {i + 1}$,我们令 $k = |x _ {i + 1} – x _ i|$,然后去判断 $gcd(n, k)$是否等于 $1$,如果不等于 $1$那么 $gcd(n, k)$就是 $n$的一个因数,返回即可
如果 $gcd(n, k) = 1$,那就生成 $x _ {i + 2}$,再进行下一轮检测
由于 $x _ i$完全由 $x _ {i – 1}$决定,因此环是一定存在的,而且大概长这样:
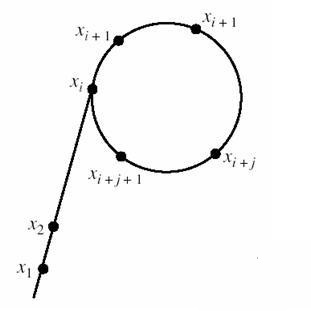
看起来就像 $\rho$,所以算法名叫 “rho”
出现环了都还没找到就说明用当前的 $x$数组是无论如何也找不到正确的 $k$的了,因此直接返回
找环有两种,一种是 floyd 判环,一种是 brent 判环,brent 判环更优秀一些
floyd 判环就是设 $a = x _ i$,$b = x _ {2i}$,每次判断 $gcd(n, |a – b|)$,当 $a = b$时说明已经出现了环
而 brent 判环是每次 $a = x _ {2 ^ i}, b = x _ {2 ^ i + j}(j < 2 ^ i)$,即 $b$在 $x _ 1, x _ 2, x _ 3 …$中这样枚举,初始时 $a = x _ 0$,然后当 $b = x _ {2 ^ i} + 1$时,就把 $a$更新成 $x _ {2 ^ i}$,然后检测 $|a – b|$。
听起来很玄学,我也没去证明复杂度,维基百科上有 OvO…
模板:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL mul(LL a, LL b, LL M)
{
a = a % M, b = b % M;
return ((a * b - (LL)(((long double) a * b + 0.5) / M) * M) % M + M) % M;
}
template<typename _Tp> inline void IN(_Tp& dig)
{
char c; bool flag = 0; dig = 0;
while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
if (flag) dig = -dig;
}
LL Rand() {return ((LL)rand() << 30) ^ rand();}
int testcase;
LL n, ans;
LL qpow(LL a, LL b, LL p)
{
LL res = 1;
while (b)
{
if (b & 1) res = mul(res, a, p);
a = mul(a, a, p), b >>= 1;
}
return res % p;
}
bool mr(LL p) // miller-rabin
{
if (p < 2) return 0;
if (p == 2) return 1;
if (!(p & 1)) return 0;
LL k = p - 1; int t = 0;
while (!(k & 1)) k >>= 1, t++;
for (int C = 1; C <= 6; C += 1)
{
LL a = Rand() % (p - 2) + 2, s = qpow(a, k, p), l = s;
for (int i = 1; i <= t; i += 1)
{
s = mul(s, s, p);
if (s == 1 && l != 1 && l != p - 1) return 0;
l = s;
}
if (s != 1) return 0;
}
return 1;
}
LL gcd(LL a, LL b) {return b ? gcd(b, a % b) : a;}
LL pr(LL a, LL c) // pollard's rho
{
LL x = 2, y = 2, d = 1, k = 0, u = 1;
c %= a;
while (d == 1)
{
k++, x = (mul(x, x, a) + c) % a;
d = gcd(x > y ? x - y : y - x, a);
if (k == u) y = x, u <<= 1;
}
return d == a ? pr(a, Rand()) : d;
}
void dfs(LL a) // 这个只是寻找最大质因子
{
if (a <= ans) return;
if (mr(a)) {ans = a; return;}
LL d = pr(a, Rand());
while (a % d == 0) a /= d;
if (a < d) swap(a, d);
dfs(a), dfs(d);
}
int main(int argc, char const* argv[])
{
IN(testcase), srand(2198731);
while (testcase--)
{
IN(n);
if (mr(n)) puts("Prime");
else ans = 0, dfs(n), printf("%lld\n", ans);
}
return 0;
}
然后你会发现在 Luogu 的 【模板】Pollard-Rho 算法中这个代码会 TLE,那怎么办呢,它卡常啊
我暂时还没啥办法,打表呗
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL mul(LL a, LL b, LL M)
{
a = a % M, b = b % M;
return ((a * b - (LL)(((long double) a * b + 0.5) / M) * M) % M + M) % M;
}
template<typename _Tp> inline void IN(_Tp& dig)
{
char c; bool flag = 0; dig = 0;
while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
if (flag) dig = -dig;
}
LL Rand() {return ((LL)rand() << 30) ^ rand();}
int testcase;
LL n, ans;
LL qpow(LL a, LL b, LL p)
{
LL res = 1;
while (b)
{
if (b & 1) res = mul(res, a, p);
a = mul(a, a, p), b >>= 1;
}
return res % p;
}
bool mr(LL p)
{
if (p < 2) return 0;
if (p == 2) return 1;
if (!(p & 1)) return 0;
LL k = p - 1; int t = 0;
while (!(k & 1)) k >>= 1, t++;
for (int C = 1; C <= 6; C += 1)
{
LL a = Rand() % (p - 2) + 2, s = qpow(a, k, p), l = s;
for (int i = 1; i <= t; i += 1)
{
s = mul(s, s, p);
if (s == 1 && l != 1 && l != p - 1) return 0;
l = s;
}
if (s != 1) return 0;
}
return 1;
}
LL gcd(LL a, LL b) {return b ? gcd(b, a % b) : a;}
LL pr(LL a, LL c)
{
LL x = 2, y = 2, d = 1, k = 0, u = 1;
c %= a;
while (d == 1)
{
k++, x = (mul(x, x, a) + c) % a;
d = gcd(x > y ? x - y : y - x, a);
if (k == u) y = x, u <<= 1;
}
return d == a ? pr(a, Rand()) : d;
}
void dfs(LL a)
{
if (a <= ans) return;
if (mr(a)) {ans = a; return;}
LL d = pr(a, Rand());
while (a % d == 0) a /= d;
if (a < d) swap(a, d);
dfs(a), dfs(d);
}
void goFuckYourself()
{
puts("999538481\n999631723\n999698731\n999605221\n999728819\n999155401\n999981403\n999477667\n999879677\n999887227\n999469249\n999581519\n999593293\n999812767\n999516761\n999781567\n999845017\n999918151\n999729977\n999527033\n999739463\n999455851\n999840367\n999342457\n999793789\n999878683\n999943969\n999625541\n999624253\n999909013\n999696371\n999488353\n999869081\n999617681\n999137371\n999908957\n999739729\n999271319\n999918343\n999969307\n999937513\n999700043\n999972871\n999552511\n999837607\n999899809\n999413033\n999774241\n999423533\n999202901\n999488657\n999949427\n999303551\n999845111\n999754477\n999679189\n999337279\n999678443\n999790633\n999172169\n999131893\n999958217\n999646391\n999990851\n999549679\n999978869\n999190733\n999751009\n999157273\n999423629\n999904331\n999580243\n999209621\n999444869\n999936391\n999471547\n999963131\n999983521\n999293879\n999425939\n999865411\n999182579\n999849689\n999495493\n999857641\n999988007\n999926843\n999801893\n999303583\n999516823\n999985097\n999341869\n999276001\n999667589\n999601903\n999654983\n999710729\n999744091\n999677513\n999877673\n999987323\n999536987\n999202517\n999633449\n999807979\n999823051\n999281867\n999877699\n999530027\n999328021\n999435109\n999845953\n999803341\n999995431\n999798647\n999243019\n999743977\n999523913\n999517027\n999560449\n999336713\n999273941\n999869069\n999721337\n999755381\n999617687\n999991123\n999732157\n999430651\n999365483\n999979859\n999941203\n999908843\n999856789\n999728039\n999788809\n999941843\n999879071\n999152813\n999506987\n999949141\n999386249\n999356333\n999999043\n999704003\n999932671\n999637777\n999965147\n999134509\n999853847\n999934031\n999889733\n999382679\n999887489\n999807397\n999884959\n999955163\n999242551\n999972277\n999639649\n999659629\n999949037\n999859603\n999392441\n999565709\n999957083\n999889519\n999885779\n999815491\n999770143\n999735703\n999997133\n999867007\n999998683\n999851761\n999868769\n999397153\n999149237\n999322187\n999863927\n999696371\n999878771\n999607801\n999606719\n999658733\n999866587\n999880367\n999920687\n999771083\n999578857\n999276017\n999885017\n999419009\n999924803\n999168281\n999331211\n999682183\n999774121\n999367619\n999489877\n999862033\n999368893\n999500503\n999429247\n999697997\n999855809\n999912007\n999903379\n999432253\n999682469\n999745613\n999729373\n999815149\n999324607\n999556249\n999866071\n999446263\n999679139\n999920953\n999778673\n999641911\n999917117\n999416963\n999217673\n999879953\n999945173\n999992977\n999222017\n999680389\n999598429\n999305873\n999840031\n999929449\n999912211\n999669929\n999975841\n999346549\n999682417\n999669607\n999654373\n999694303\n999776573\n999987601\n999961387\n999680153\n999590309\n999816791\n999927427\n999801721\n999453527\n999583367\n999457757\n999710197\n999631393\n999881977\n999649933\n999506477\n999902933\n999546701\n999819797\n999482093\n999984043\n999263423\n999779699\n999661777\n999794863\n999546571\n999966601\n999405749\n999939947\n999618509\n999758653\n999561191\n999781799\n999801893\n999824083\n999729827\n999871283\n999879737\n999597563\n999296483\n999480817\n999279031\n999311683\n999988547\n999618817\n999305137\n999671297\n999929417\n999399971\n999873869\n999551743\n999390361\n999847903\n999921829\n999880477\n999724651\n999998269\n999784537\n999908423\n999860111\n999299687\n999079421\n999351329\n999537269\n999678019\n999631519\n999355993\n999995813\n999777379\n999817129\n999916717\n999412079\n999688223\n999507893\n999895999\n999985969\n999360643\n999438059\n999820909\n999582109\n999832807\n999655757\n999695303\n999912007\n999861637\n999653587\n999488159\n999212329\n999999607\n999934723\n999395629\n999868799\n999816617\n999883483\n999083471\n999501967\n999060047\n999998653\n999553333\n999583439\n999958829\n999978103\n999767303\n999919699\n999841523\n999966997\n999445039\n999693043\n999930647");
}
int main(int argc, char const* argv[])
{
IN(testcase), srand(2198731);
while (testcase--)
{
IN(n);
if (testcase == 349 && n == 998773295310793741ll)
goFuckYourself(), exit(0);
if (mr(n)) puts("Prime");
else ans = 0, dfs(n), printf("%lld\n", ans);
}
return 0;
}
0 条评论