什么是 2-SAT?
SAT 是适定性(Satisfiability)问题的简称。一般形式为 k – 适定性问题,简称 k-SAT。而当 $k > 2$ 时该问题为 NP 完全的。所以我们只研究 $k = 2$ 的情况。
简单来说的话就是有 $n$个变量 $x _ 1, x _ 2, x _ 3, …, x _ n$,取值为 $0$或 $1$,即这是 $n$个布尔型变量
现在给出 $m$个约束条件,例如 $x _ a \wedge x _ b = 0$(其中 $\wedge $符号逻辑与)
最后问是否有解使得 $x$之间满足给出的约束,若有解则输出一组解
这就是一个非常典型的 2-SAT 问题
如何解决
就给出的例子来讲,假如 $n = 3$,我们可以构造如下的图:
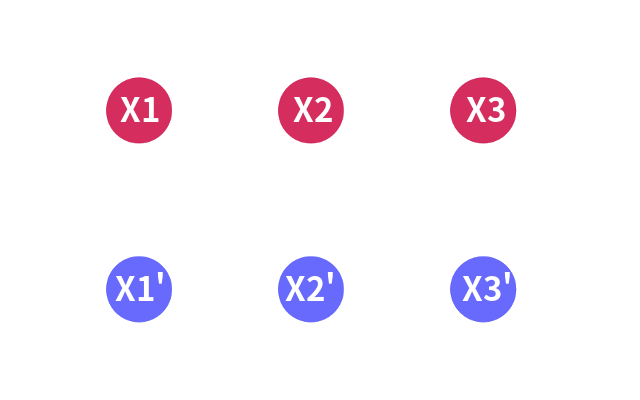
其中 $X _ 1, X _ 1’$为一对,$X _ 2, X _ 2’$为一对,$X _ 3, X _ 3’$为一对,分别表示 $x _ 1, x _ 2, x _ 3$的取值
怎么表示呢?
每一对点中我们都选中其中一个,选中了红色的 $X _ 1$就表示 $x _ 1$的取值为 $1$,选中了蓝色的 $X _ 1’$就表示 $x _ 1$的取值为 $0$
假设有一个约束条件:$x _ 1 \wedge x _ 2 = 0$
那么就从 $X _ 1$向 $X _ 2’$连一条有向边,从 $X _ 2$向 $X _ 1’$连一条有向边
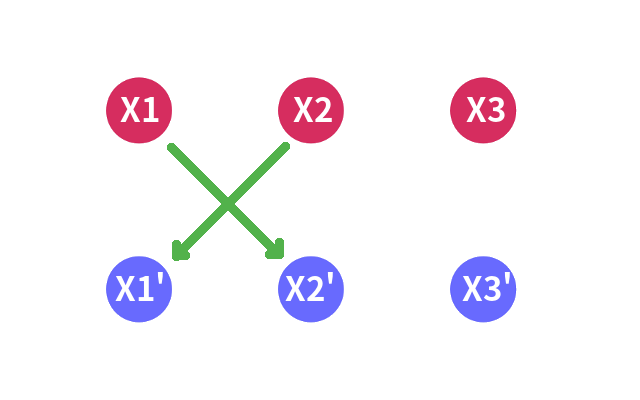
从点 $a$向点 $b$连一条有向边的意义是:选点 $a$则一定选点 $b$,但选点 $b$不一定选点 $a$
这样连边以后你会发现:
如果我们想让 $x _ 1 = 1$,那么我们就要选择 $X _ 1$,然后就必须要选择 $X _ 2’$,这样 $x _ 2$就 $= 0$了。
同理,如果 $x _ 2 = 1$,那么 $x _ 1$就一定 $= 0$
但是当 $x _ 1 = 0$时,$x _ 2$的取值是不受限制的,反过来同理
这样我们就巧妙地实现了这个约束
现在再加入一个条件,$x _ 2 \vee x _ 3 = 1$,其中 $\vee$符号表示逻辑或
那就这样连边咯:
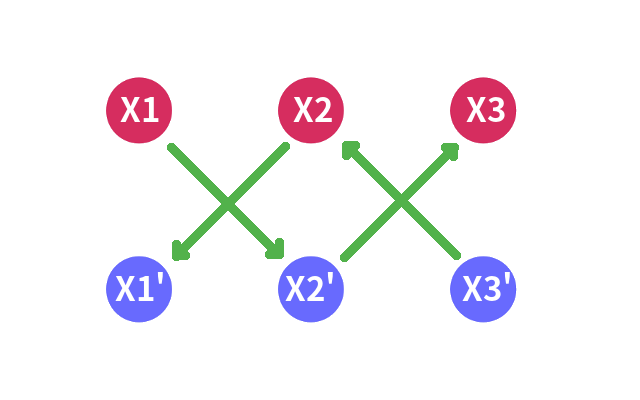
对着图验证一下,我们会发现所有满足图中关系的选点方式对应的那个解也是满足条件的。
算法
于是现在的问题转化成了图上选点问题,没对点中选一个,需要满足被选择的点集没有边是连向没被选的点集的
首先求强连通分量,如果 $X _ i$与 $X _ i’$同属于一个强连通分量,那就一定无解,因为这样你必须同时选择 $X _ i$和 $X _ i’$,这样你就 GG 了
假如不存在这种情况,那就一定有解。
如果需要你输出任意一组解,只需要把缩点后的图进行一遍拓扑排序,$X _ i$和 $X _ i’$中选择所在强连通分量的拓扑序大的那一个即可
因为如果两者之间毫无关联,根本没有一条路径联通它俩,那选谁都随便
如果有,那只能选择拓扑序大的
因此我们就选择拓扑序大的咯
拓展:
这时候可能有疑问了:
比如这个例子:
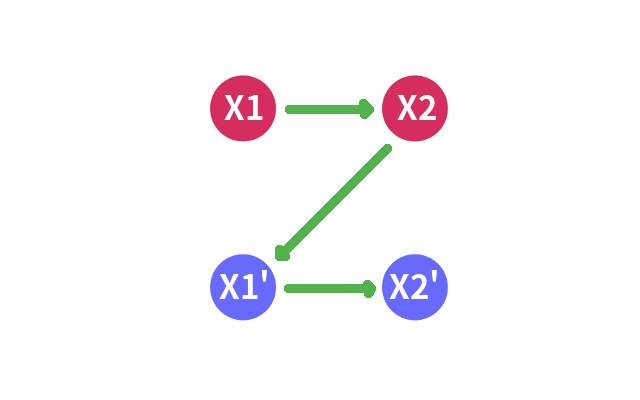
这个例子中没有两个点在同一个强连通分量中,但是确实无解
会不会出现这种情况呢?
答案是不会的,至少做题的时候不会出现
因为 2-SAT 是有对称性的,不可能构造出这样的图
然后其实没必要进行拓扑排序,因为 Tarjan 求出的强连通分量的编号就是拓扑序反序(画画图就知道了)
这样 2-SAT 问题就解决了
当然有时候题目可能要你输出什么字典序最小的解啊啥的,那就只能暴力 dfs,枚举某对点中选择谁,然后把它延伸出去的点全染色,具体就不赘述了
例题
1. Panda’s Trick POJ – 3207
题意:
把一个圆 $n$等分,等分点顺时针编号为 $0, 1, 2, 3, …, n$
现在要在 $m$对点对之间各连一条线,可以是直线也可以是曲线,可以在圆内也可以在圆外
问是否存在一种连线方式,使得这 $m$条线没有交点
$n \leq 1000, m \leq 500$
嗯,如果不跟我说我觉得我很难想到 2-SAT
对于每对点,它们之间的连线可以在圆内,也可以在圆外(显然不会有在圆内外穿来穿去的奇妙线条),这就是一对状态
如果两对点,它们在圆内的线条会相交,那么它们必须是一对点的线在圆内,另一对在圆外(两个都在圆外也一定会相交)
这个就相当于 $m$对 $x _ i \not = x _ j$的约束
那么就这样连边:
$X _ i -> X _ j’$
$X _ i’ -> X _ j$
$X _ j – > X _ i’$
$X _ j’ -> X _ i$
然后染色就行啦!
#include <cstdio>
#include <cctype>
#include <cstring>
#include <stack>
#include <algorithm>
#define NS (2005)
#define MS (500000)
using namespace std;
template<typename _Tp> inline void IN(_Tp& dig)
{
char c; bool flag = 0; dig = 0;
while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
if (flag) dig = -dig;
}
int n, m, X[NS], Y[NS], col[NS], cnt;
struct graph
{
int head[NS], nxt[MS], to[MS], sz;
void init() { memset(head, -1, sizeof(head)), sz = 0; }
graph() { init(); }
void push(int a, int b)
{
nxt[sz] = head[a], to[sz] = b, head[a] = sz++;
}
int operator [] (const int a) const { return to[a]; }
} g;
void dfs(int a)
{
col[a] = cnt;
for (int i = g.head[a]; ~i; i = g.nxt[i])
if (!col[g[i]]) dfs(g[i]);
}
int main(int argc, char const* argv[])
{
while (~scanf("%d%d", &n, &m))
{
for (int i = 1; i <= m; i += 1)
{
IN(X[i]), IN(Y[i]);
if (X[i] > Y[i]) swap(X[i], Y[i]);
}
for (int i = 1; i <= m; i += 1)
for (int j = i + 1; j <= m; j += 1)
{
if (X[i] == X[j] || Y[i] == Y[j])
{
puts("the evil panda is lying again");
goto end;
}
int a = i, b = j;
if (X[a] > X[b]) swap(a, b);
if (X[b] < Y[a] && Y[a] < Y[b])
{
g.push(a << 1, b << 1 | 1), g.push(b << 1 | 1, a << 1);
g.push(b << 1, a << 1 | 1), g.push(a << 1 | 1, b << 1);
}
}
for (int i = 1; i <= m; i += 1)
{
if (!col[i << 1]) cnt++, dfs(i << 1);
if (!col[i << 1 | 1]) cnt++, dfs(i << 1 | 1);
}
for (int i = 1; i <= m; i += 1)
if (col[i << 1] == col[i << 1 | 1])
{
puts("the evil panda is lying again");
goto end;
}
puts("panda is telling the truth...");
end : g.init(), memset(col, 0, sizeof(col)), cnt = 0;
}
return 0;
}
2. Wedding POJ – 3648
题面很奇妙
题目大意:
一对新人结婚,有一个长桌,新郎坐一边,新娘做他对面。除了新郎新娘,还有 $n – 1$对夫妻。但有趣的是,这 $2n$个人存在着奇妙の通奸关系,比如第二对夫妻的丈夫可能与第三对夫妻的妻子存在通奸关系,也可能与第三对夫妻的丈夫存在通奸关系(贫穷限制了我的想象力)。每对夫妻都是面对面坐的,不会坐在同一边。
新娘很讲究,她不希望看到她对面,也就是新郎坐的那一边,存在任意一对有通奸关系的人(我就好奇她怎么谁有通奸关系都知道)
她想知道,是否存在满足她要求的座位安排方式,若存在还需要输出任意一种安排方式
(编号从 $0$开始,结婚的新人是第 $0$对夫妻)
$n \leq 30$
嗯,抛开题面不谈,这就是裸的 2-SAT
每对夫妻就是一个变量,选 $1$是丈夫坐在新郎那边,选 $0$是妻子坐在新郎那边
因为要求是对新郎那边定义的,因此新郎一定要选,所以从 $X _ 0’$(妻子)连一条边到 $X _ 1’$(丈夫),这样丈夫就必选了
然后对于一个通奸关系,也就是要求两者的选择状态与起来 $= 0$
比如第一对的丈夫和第二对的妻子有通奸关系,那就这样连边:
$X _ 1 -> X _ 2$
$X _ 2′ -> X _ 1’$
嗯,然后 Tarjan 缩点搞搞就行了
#include <cstdio>
#include <cctype>
#include <cstring>
#include <stack>
#include <algorithm>
#define NS (65)
#define MS (3605)
using namespace std;
int n, m, id[NS], low[NS], dfn, scc[NS], cnt;
stack<int> st;
bool ins[NS];
struct graph
{
int head[NS], nxt[MS], to[MS], sz;
void init() { memset(head, -1, sizeof(head)), sz = 0; }
graph() { init(); }
void push(int a, int b)
{
nxt[sz] = head[a], to[sz] = b, head[a] = sz++;
}
int operator [] (const int a) const { return to[a]; }
} g;
void tarjan(int a)
{
id[a] = low[a] = ++dfn, st.push(a), ins[a] = 1;
for (int i = g.head[a]; ~i; i = g.nxt[i])
if (!id[g[i]]) tarjan(g[i]), low[a] = min(low[a], low[g[i]]);
else if (ins[g[i]]) low[a] = min(low[a], id[g[i]]);
if (id[a] == low[a])
{
scc[a] = ++cnt;
while (st.top() != a)
scc[st.top()] = cnt, ins[st.top()] = 0, st.pop();
ins[a] = 0, st.pop();
}
}
int main(int argc, char const* argv[])
{
while (scanf("%d%d", &n, &m), n || m)
{
for (int i = 1, a, b; i <= m; i += 1)
{
char ac, bc;
scanf("%d%c%d%c", &a, &ac, &b, &bc);
a++, b++, a <<= 1, b <<= 1;
if (ac == 'w') a |= 1;
if (bc == 'w') b |= 1;
g.push(a, b ^ 1), g.push(b, a ^ 1);
}
g.push(3, 2);
for (int i = 1; i <= n; i += 1)
{
if (!id[i << 1]) tarjan(i << 1);
if (!id[i << 1 | 1]) tarjan(i << 1 | 1);
}
for (int i = 1; i <= n; i += 1)
if (scc[i << 1] == scc[i << 1 | 1])
{ puts("bad luck"); goto end; }
for (int i = 2; i <= n; i += 1)
if (scc[i << 1] < scc[i << 1 | 1]) printf("%dw ", i - 1);
else printf("%dh ", i - 1);
putchar(10);
end : g.init(), memset(id, 0, sizeof(id)), dfn = cnt = 0;
}
return 0;
}
0 条评论