// 这题是个双倍经验题,另一道是 BZOJ – 4398 福慧双修
比较奇妙的做法,记录一下
这题正解有两个,第一个是一个 $\log$的重构图法,还有一个是两个 $\log$的二进制分组法,都很强。
今天考试刚好考到这题,大部分 AC 的同学用的都是二进制分组法,也就是每次按二进制分为两组,一组只出不进,另一组只进不出,这样就能保证枚举到所有答案了
但这样复杂度较高,一秒钟跑出来有点吃力(在比较慢的机子上),于是只能减小枚举次数,用正确率换取时间
我考场上瞎 YY 了一个非常奇妙的做法——迭代最短路:
为了方便我们把所有和出发点有边相连的点编号为 $1, 2, 3, …, k$
首先暴力做法就是每次选定一个与出发点相连的点,令它返回出发点的边长度为正无穷,然后从它开始跑最短路,最后取每次最短路的最小值
但这样我们能发现我们做了很多无用功:
比如我们当前选定了点 $2$,假如点 $2$到点 $a$的最短路长度大于点 $1$到点 $a$的最短路长度,那么其实没有必要继续从点 $a$向外扩展了,因为这样扩展出来的路径 $2->a->b$一定不如 $1->a->b$
因此每次跑完最短路是没有必要清空 $dis$数组的,跑完点 $1$的最短路就直接开始跑点 $2$的最短路、点 $3$的最短路,依次类推
当然值得注意的是这样我们只会计算出 $i->j (i < j)$的最短路那么对于 $(i > j)$的最短路我们还要把编号反过来重新跑一遍,即先算点 $k$的最短路,然后点 $k – 1, k – 2, …$这样算完了就能保证所有答案都被考虑到了,正确性很显然是对的
那么复杂度呢?如果最短路用迪杰斯特拉这样复杂度看起来大概是 $O(n m \log _ 2 n)$的,妥妥的超时啊
但是实测它跑得飞快,比二进制分组不知道快到哪里去了,和正解的一个 $\log$的重构图差不多
(警告:伪证明开始)
仔细一想:期望下下降子序列长度是 $\log n$的
其实用 “下降子序列” 这个形容词可能并不准确,准确地说是 “单调递减单调栈的最终长度”
也就是说一开始给那 $k$个点随机编号(注意要随机,不然可以被卡,random_shuffle 一下就行了),那么依次选点,每个点能更新的后继节点数期望是 $\log n$的
这样复杂度大概是 $O(m \log ^ 2 n)$
另外我还加了一个剪枝,就是如果当前点 $dis + $到起点的最近距离大于等于当前的最优解了就直接 continue
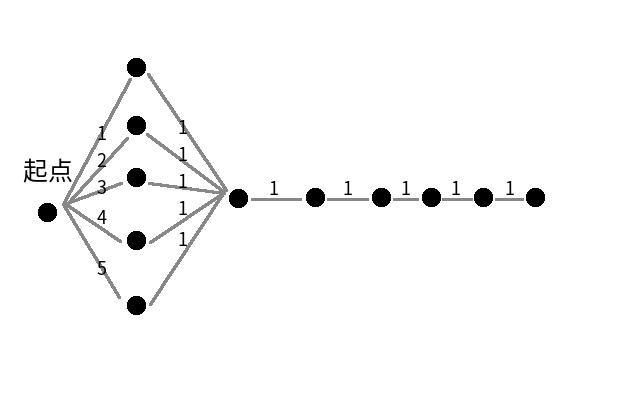
一般的数据其实根本达不到这个复杂度,我想了一种构造的方法:
分 $\frac n 2$个点用来和起点相连,剩下 $\frac n 2$个点排成一条链
起点的出边边权依次增大,链上的边权全部为 $1$,图弄出来大概长这样:
数据生成器:
#include <bits/stdc++.h>
using namespace std;
int n = 10000, m, N, X[1000000], Y[1000000], A[1000000], B[1000000];
int main(int argc, char const* argv[])
{
N = n >> 1;
for (int i = 1; i <= N; i += 1)
{
X[++m] = 1, Y[m] = 1 + i, A[m] = i, B[m] = 10000;
X[++m] = 1 + i, Y[m] = N + 2, A[m] = 1, B[m] = 10000;
}
for (int i = N + 3; i <= n; i += 1)
X[++m] = i - 1, Y[m] = i, A[m] = B[m] = 1;
while (m < 200000)
X[++m] = n, Y[m] = rand() % N + 2, A[m] = 10000, B[m] = 10000;
printf("%d %d\n", n, m);
for (int i = 1; i <= m; i += 1)
printf("%d %d %d %d\n", X[i], Y[i], A[i], B[i]);
return 0;
}
这样每次 $k$个点中一旦有一个点能更新后继节点,那它就会把整张图都更新一遍
这样可以把复杂度卡到 $O(m \log ^ 2 n)$
然而算法还是跑得非常快 _(:зゝ∠)_
具体复杂度上限是不是 $O(m \log ^ 2 n)$我也不太清楚,我(和 boshi)猜是这样的
悬赏 10 块钱哟,卡掉这个算法的我就给他 10 块钱哟~(长期有效)
代码:
#include <bits/stdc++.h>
#define NS (10005)
#define MS (400005)
using namespace std;
typedef pair<int, int> PII;
template<typename _Tp> inline void IN(_Tp &dig)
{
char c; bool flag = 0; dig = 0;
while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
if (flag) dig = -dig;
}
int n, m, O[NS], I[NS], Q[NS], ans = INT_MAX;
struct graph
{
int head[NS], nxt[MS], to[MS], w[MS], sz;
graph() { memset(head, -1, sizeof(head)), sz = 0; }
inline void push(int a, int b, int c)
{
nxt[sz] = head[a], to[sz] = b, w[sz] = c, head[a] = sz++;
}
inline int operator [] (const int a) const { return to[a]; }
} g;
struct heap
{
PII v[MS];
int sz;
inline PII &operator [] (const int a) { return v[a]; }
inline void push(const PII a)
{
v[sz++] = a, push_heap(v, v + sz, greater<PII>());
}
inline void pop()
{
pop_heap(v, v + sz, greater<PII>()), sz--;
}
} pq;
int dis[NS];
bool book[NS];
void dij(int u)
{
book[u] = 0, pq.push(PII(dis[u], u));
while (pq.sz)
{
int a = pq[0].second; pq.pop();
if (book[a]) continue;
book[a] = 1;
if (I[0] + dis[a] >= ans) continue;
if (a != u && I[a]) ans = min(ans, I[a] + dis[a]);
for (int i = g.head[a]; ~i; i = g.nxt[i])
if (dis[g[i]] > dis[a] + g.w[i])
{
book[g[i]] = 0;
dis[g[i]] = dis[a] + g.w[i];
pq.push(PII(dis[g[i]], g[i]));
}
}
}
inline void run()
{
memset(dis + 1, 127, sizeof(int) * n);
for (int i = 1; i < n; i += 1)
if (O[Q[i]] && dis[Q[i]] > O[Q[i]]) dis[Q[i]] = O[Q[i]], dij(Q[i]);
}
int main(int argc, char const* argv[])
{
srand(19260817), IN(n), IN(m);
for (int i = 1, a, b, c, d; i <= m; i += 1)
{
IN(a), IN(b), IN(c), IN(d);
if (a > b) swap(a, b), swap(c, d);
if (a == 1)
{
if (O[b])
{
ans = min(ans, min(O[b] + d, c + I[b]));
O[b] = min(O[b], c), I[b] = min(I[b], d);
}
else O[b] = c, I[b] = d;
I[0] = min(I[0], I[b]);
}
else g.push(a, b, c), g.push(b, a, d);
}
for (int i = 2; i <= n; i += 1) Q[i - 1] = i;
random_shuffle(Q + 1, Q + n);
run(), reverse(Q + 1, Q + n), run();
printf("%d\n", ans);
return 0;
}
另外还有一个有趣的事情:
psb 同学考场写了个只加了 $dis \geq ans$就 continue 的优化也 AC 了,于是就被我针对了。
那样的算法可以被分层图卡掉,第 $i$层到第 $i + 1$层的对应点连一条出的距离为 $1$,入的距离为 $10 ^ 4$的边,第 $i$层之间相邻两个点连一条出入长度都为 $1$的边,然后从起点向第一层每个点都连一条长度为 $1$的边
搞 $10$层差不多了
这样那个剪枝就没用了,最短路会更新每个点一遍
如果怕有加计数器之类的操作可以让起点到第一层都连长度为 $2$的边,然后随机一个第一层的点连一条长度为 $1$的边,这样随机的正确率就很低了
数据生成器:
#include <bits/stdc++.h>
using namespace std;
int n = 9001, m, N = 1000, p = 1, cnt = 1;
int X[1000000], Y[1000000], A[1000000], B[1000000];
int main(int argc, char const* argv[])
{
srand(time(0));
int psb = rand() % N + 1;
for(int i = 1; i <= N; i += 1)
X[++m] = 1, Y[m] = ++p, A[m] = 2 - (i == psb), B[m] = 10000;
while (n - p >= N)
{
for(int i = 1; i <= N; i += 1)
p++, X[++m] = p - N, Y[m] = p, A[m] = 1, B[m] = 10000;
for(int i = 1; i < N; i += 1)
X[++m] = p - i, Y[m] = p, A[m] = p - i, B[m] = p - i + 1;
}
printf("%d %d\n", n, m);
for (int i = 1; i <= m; i += 1)
printf("%d %d %d %d\n", X[i], Y[i], A[i], B[i]);
return 0;
}
0 条评论