刚了解很不熟练，有问题请及时指出 QAQ

带花树

带花树通常用于解决一般图最大匹配问题。

至于一般图最大权匹配问题，毒瘤请移步这里。

考虑如何处理奇环，让环上的点两两匹配，总会剩下一个点，而且每一个环上的点都存在一种环上匹配方案使得该点被剩下，那么考虑将环缩成点，缩完的点一样可以匹配。

如果要支持输出方案，那么是不能实质缩点的，用并查集即可。

定义匹配的一对点分别为黑点和白点。

算法流程：

• 从一个没有匹配出发，初始定义该点的颜色为黑。

  for(int i=1;i<=n;++i) if(!match[i]&&solve(i)) ++ans;
  

• 每一次从队列里取出节点 $u$ 进行更新：
  • 如果相邻点 $v$ 在当前轮还没有被染色

  • 如果 $v$ 被匹配了

    那么将匹配拆散，$v$ 当前为白点，将其匹配的点染成黑点，并扔进队列继续匹配，如果 $v$ 的匹配点找到了合适的匹配，那么 $v$ 可以和当前的起点 $i$ 匹配，将多增加一组匹配。

    q.push(match[v]),col[match[v]]=1;
    

  • 如果 $v$ 没有匹配

    将 $v$ 匹配给起点 $i$ ，至于怎么维护可以每一个点记录 $pre$ ，然后暴力跳链更新：

    for(int las;u;v=las,u=pre[v])
      las=match[u],match[u]=v,match[v]=u;   
    return true;
    

  • 如果相邻点 $v$ 的颜色是白

  那么不用管，因为遇见了一个偶环。

  • 如果相邻点 $v$ 的颜色是黑

  • 如果 $v$ 和 $u$ 已经是同一个花里的了

    那么不用管。

  • 否则

    暴力开花，先找到 $lca$ ，显然花将包括 $u$ 到 $v$ 路径上的所有点 (花)。

    找到 $lca$ 后，分别从 $u$ 和 $v$ 开始往上面跳，并更新 $pre$ ，由于是花，花内的 $pre$ 一定是双向的，跳的时候还需要检查颜色，如果跳到的点 $x$ 是白色，那么染色为黑扔进队列，因为将花看做点的话是可以往外面匹配的，由于我们不确定是花中的哪个节点往外匹配，故均染色为黑。

    注意跳的时候还需要更新并查集的 $fa$ 。

带花树的时间复杂度是 $O(n^3)$ 的，但在实际实现中跑不到上界，因此一般 $n=1000$ 也能跑跑。

关于跳 $lca$ 和开花两个部分没看懂 (代码) 的建议画画图：

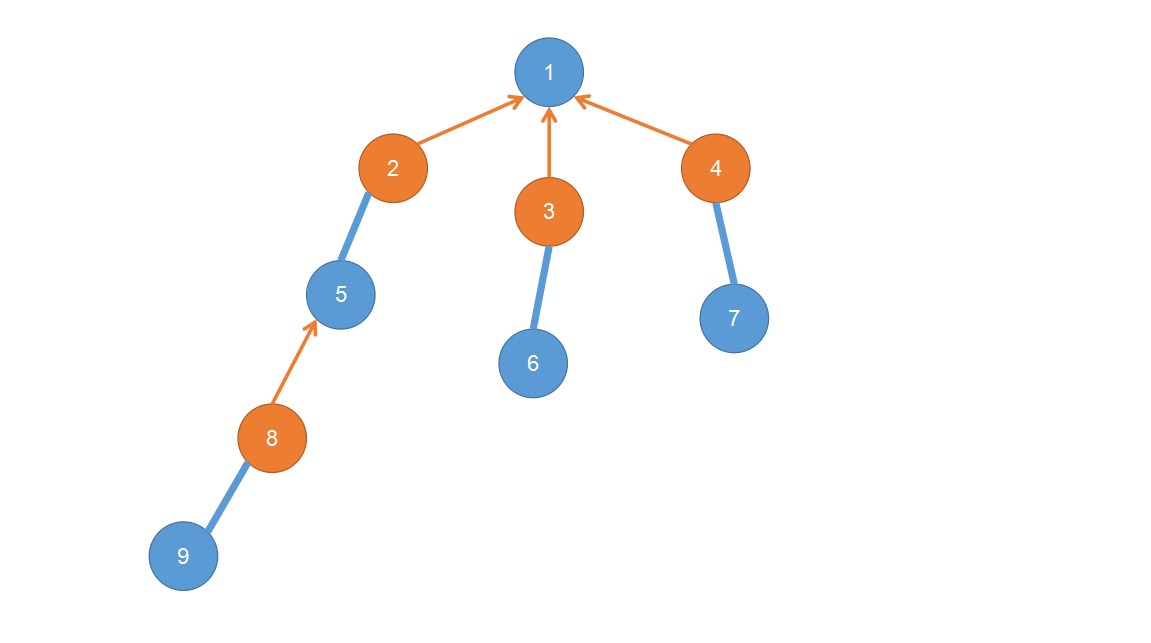
蓝点即为黑点，橙点即为白点，粗边即为匹配，有向的细边其实就是 $pre$ 指针。

---

一些题目

Luogu-P6113 一般图最大匹配
UOJ #79. 一般图最大匹配

模板题。

$\rm{Code_1:}$

namespace _ {
    queue <int> q;
    int tim,fa[N],vis[N],pre[N],col[N],match[N];
    inline int find(int x) {
        while(x!=fa[x]) x=fa[x]=fa[fa[x]];
        return x;
    }
    inline int lca(int x,int y) {
        ++tim,x=find(x),y=find(y);
        for(;;swap(x,y)) {
            if(!x) continue;
            if(vis[x]==tim) return x;
            vis[x]=tim,x=match[x]?find(pre[match[x]]):0;
        }
    }
    inline void blossom(int x,int y,int t) {
        while(find(x)!=t) {
            pre[x]=y,y=match[x];
            if(col[y]==2) col[y]=1,q.push(y);
            fa[x]=fa[y]=t,x=pre[y];
        }
    }
    inline bool solve(int s) {
        memset(pre,0,sizeof(pre));
        memset(col,0,sizeof(col));
        for(int i=1;i<=n;++i) fa[i]=i;
        while(!q.empty()) q.pop();
        q.push(s),col[s]=1;
        while(!q.empty()) {
            int u=q.front();q.pop();
            for(int v:G[u]) {
                if(!col[v]) {
                    col[v]=2,pre[v]=u;
                    if(!match[v]) {
                        for(int las;u;v=las,u=pre[v])
                            las=match[u],match[u]=v,match[v]=u; 
                        return true;
                    } else q.push(match[v]),col[match[v]]=1;                    
                } else if(col[v]==1&&find(u)!=find(v)) {
                    int t=lca(u,v);
                    blossom(u,v,t),blossom(v,u,t);
                }
            }
        }
        return false;
    }

} using namespace _;

int main() {
    IN(n),IN(m);
    for(int i=1;i<=m;++i) addedge();
    for(int i=1;i<=n;++i) if(!match[i]&&solve(i)) ++ans;
    printf("%d\n",ans);
    return puts(""),0;xuyaozhuyi
} 

---

UOJ #171.「WC2016」挑战 NPC

可以将一个筐子拆成三个点，对于一个球也要和这三个点连边，并且三个点之间连边。

如果一个筐子是合法的，那么筐子的三个点之间一定存在一个匹配。

由于每一个球一定匹配，答案为最大匹配数 $-n$ 。

注意点数是 $n+m+m+m$ 而非 $n$ ，清空数组或者定义 $fa$ 时需要注意。

$\rm{Code_2:}$

namespace Flower_tree {
    queue <int> q;
    int tim,fa[N],vis[N],pre[N],col[N],match[N];
    inline int find(int x) {
        while(x!=fa[x]) x=fa[x]=fa[fa[x]];
        return x;
    }
    inline int lca(int x,int y) {
        ++tim,x=find(x),y=find(y);
        for(;;swap(x,y)) {
            if(!x) continue;
            if(vis[x]==tim) return x;
            vis[x]=tim,x=match[x]?find(pre[match[x]]):0;
        }
    }
    inline void blossom(int x,int y,int t) {
        while(find(x)!=t) {
            pre[x]=y,y=match[x];
            if(col[y]==2) col[y]=1,q.push(y);
            fa[x]=fa[y]=t,x=pre[y];
        }
    }
    inline bool check(int s) {
        memset(pre,0,sizeof(pre));
        memset(col,0,sizeof(col));
        for(int i=1;i<=L;++i) fa[i]=i;
        while(!q.empty()) q.pop();
        q.push(s),col[s]=1;
        while(!q.empty()) {
            int u=q.front();q.pop();
            for(int v:G[u]) {
                if(!col[v]) {
                    col[v]=2,pre[v]=u;
                    if(!match[v]) {
                        for(int las;u;v=las,u=pre[v])
                            las=match[u],match[u]=v,match[v]=u; 
                        return true;
                    } else q.push(match[v]),col[match[v]]=1;                    
                } else if(col[v]==1&&find(u)!=find(v)) {
                    int t=lca(u,v);
                    blossom(u,v,t),blossom(v,u,t);
                }
            }
        }
        return false;
    }
    inline int solve() {
        int ans=0;
        for(int i=1;i<=L;++i) if(!match[i]&&check(i)) ++ans;
        return ans;
    }
} using namespace Flower_tree;

inline void Main() {
    memset(match,0,sizeof(match)),
    memset(vis,0,sizeof(vis)),tim=0;
    IN(n),IN(m),IN(e),L=n+m+m+m;
    for(int i=1;i<=L;++i) G[i].clear();
    int x,y;
    for(int i=1;i<=e;++i) {
        IN(x),IN(y);
        addedge(x,n+y),addedge(x,n+m+y),addedge(x,n+2*m+y);
    }
    for(int i=1;i<=m;++i)
        addedge(n+i,n+m+i),addedge(n+i,n+2*m+i),addedge(n+m+i,n+2*m+i);
    printf("%d\n",solve()-n);
    for(int i=1;i<=n;++i) printf("%d ",(match[i]-n-1)%m+1);
    return puts(""),void();
}

int T;
int main() {
    IN(T);
    while(T--) Main();
    return 0;
} 

---