1. 前言
如果给你一棵树,求点 u 到点 v 路径上点的权值之和,你可能会说:倍增啊!
那如果出题人:我还要你支持修改某个点的权值!
或者再 j 一点:我还要你支持修改点 u 到点 v 路径上点的权值!
那就得用树链剖分了。
2. 什么是树链剖分
上面那个问题,树上区间修改。
区间修改最常见做法就是线段树了。
那我们怎么用线段树维护一颗。。。普通的树呢?
那就给普通的树的每个节点标个号,然后放线段树里呗。区间维护。
但如果随便标号,那点 u 到点 v 路径不一定标号是连续的啊,你线段树维护个 j 啊
所以我们现在引入一个(堆)姿势:



那么这些姿势有什么用呢?先看一道题吧!

我们先来看张图:
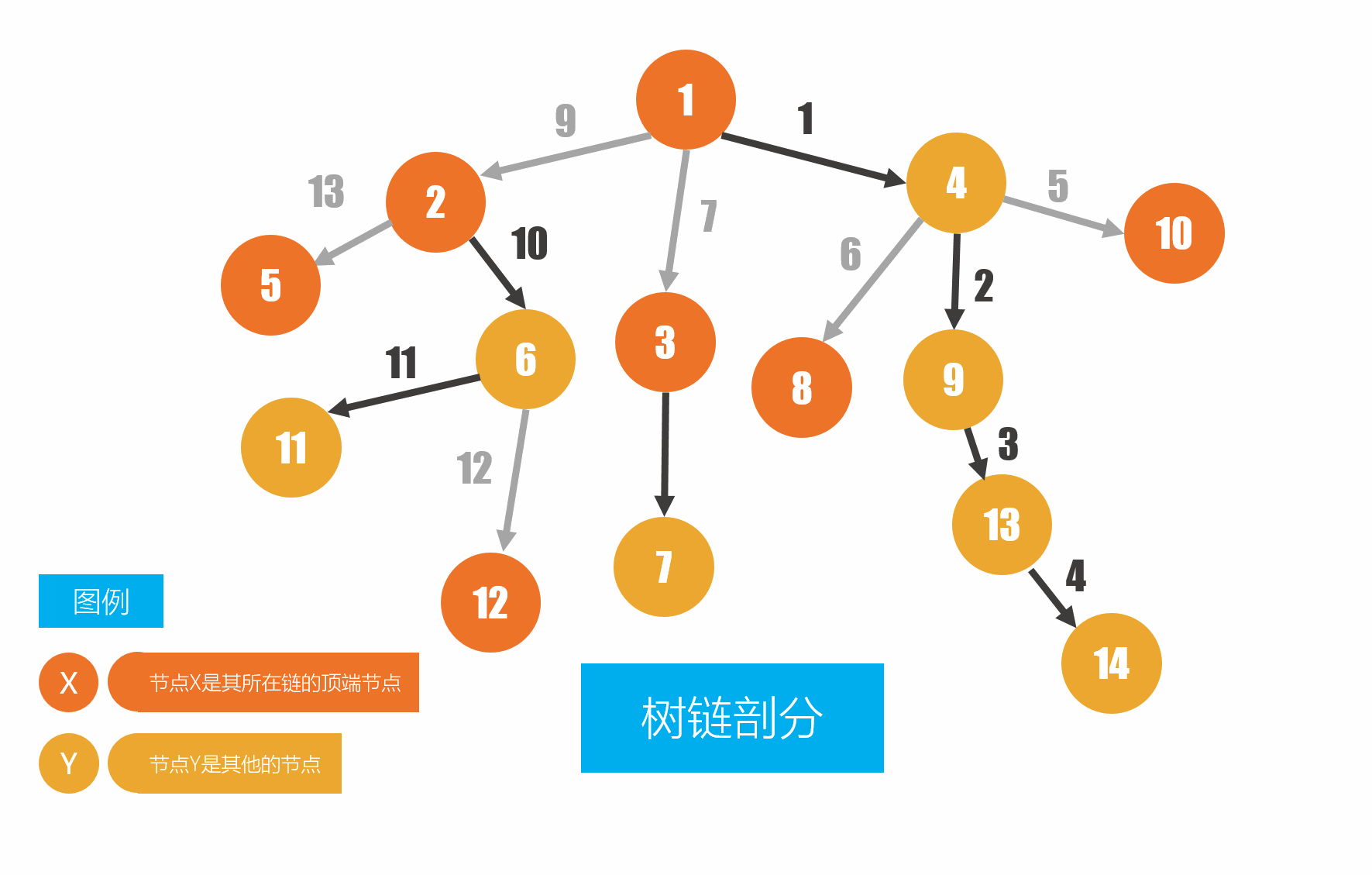
图中标在边上了,但也不影响我们学。。。
标号方法是:跑 dfs,先给当前节点标号,再给重儿子标号(重儿子和当前节点在一个重链上),然后对重儿子递归,最后给剩下的别的儿子标号(别的儿子不和当前节点在一个重链上,所以新建重链,把新建的重链的顶端节点设为那个” 别的儿子 “)、递归(图中是先给重 (zhong) 边标号,再给剩下的边标号)。标号从小到大。
不难发现一条重链上的标号是连续的,比如点 1 到点 14,点 2 到点 12
这意味着在线段树中,它们是在一个连续的区间里的,而不是像随便标号时断断续续的。
这样就很好用线段树处理了。
如果两个节点不在一条重链上呢?比如图中的点 11 和点 10,我们要求它们之间的路径上的点权和
那我们就看,点11所在的重链是11->6->2,点10所在的重链是10(10所在的重链只有一个点,就是10)。所以我们就先求出重链11->6->2 上的点权和、重链 10 上的点权和。这两条重链在线段树上都是一段连续的区间,可以直接 log2n 求出
这时候我们发现还有4->1 的重链没有计算,就把它的点权和计算出来,三个重链的点权和加在一起就得到了答案。
所以我们要记录的是:
1. pos[i] 点 i 的标号
2. top[i] 点 i 所在重链的顶端节点
3. siz[i] 以点 i 为根的子树的大小
4. dep[i] 点 i 的深度
5. fa[i] 点 i 的父亲节点
我们先跑一边 dfs,算出 fa、size、dep
然后再跑一边 dfs,根据 size[i] 找出点 i 的重儿子,然后算出 pos、top。
具体代码:
void init1(int u)//第一个 dfs
{
siz[u]=1,dep[u]=dep[fa[u]]+1;
for(int i=0;i<g[u].size();i++)//g[u] 为点 u 的邻接表
if(g[u][i]!=fa[u])fa[g[u][i]]=u,init1(g[u][i]),siz[u]+=siz[g[u][i]];//向下递归
}
void init2(int u)//第二个 dfs
{
int nxt=0,maxn=0;pos[u]=cnt++;//设置 pos[u]
for(int i=0;i<g[u].size();i++)//找出重儿子
if(g[u][i]!=fa[u]&&siz[g[u][i]]>maxn)nxt=g[u][i],maxn=siz[g[u][i]];
if(!nxt)return;//不存在重儿子就 return
top[nxt]=top[u],init2(nxt);//把重儿子加到 u 所在的重链里,然后递归重儿子
for(int i=0;i<g[u].size();i++)
if(g[u][i]!=fa[u]&&g[u][i]!=nxt)
top[g[u][i]]=g[u][i],init2(g[u][i]);//新建重链
}
搞完这些就很 easy 了,因为一段重链在线段树里是一段连续的区间(这是坠重要的)。
我们在查询/修改从点 u 到点 v 的路径时,先找到所在重链的顶端节点(top)深度较深的(因为这样能让 u 和 v 同步提升,防止一个提到根节点了,另一个还没提,这时候你就不知道提谁了),注意不能按照 u 和 v 的深度来提!比如 top 较深的点是 u,然后就用线段树处理区间 $[pos[top[u]],pos[u]]$(因为 top[u] 的标号一定比 u 要小),再设置 u 为 fa[top[u]],把 u 往上提,直至 u 和 v 在一条重链上(即 top[u]==top[v])。这时候可能 u 和 v 之间还有一段距离,此时 u 和 v 已经在一条重链上,直接处理它们之间的区间就行了。
然后复杂度就是:$O(Nlog_{2} N+Qlog^{2} N)$
同时这个复杂度也是一般的树链剖分的复杂度。因为重链个数不会超过 $log_{2} N$个,线段树复杂度是 $log_{2} N$的。网上有证明,我就不做过多赘述
代码:
#include <bits/stdc++.h>
#define LS(a) (a<<1)
#define RS(a) ((a<<1)|1)
#define NS (30005)
using namespace std;
struct N{int l,r,max,sum;N(){l=r=max=sum=0;}}e[NS<<2];
int n,fa[NS],dep[NS],siz[NS],pos[NS],top[NS],w[NS],cnt=1,q;
char opt[10];
vector<int> g[NS];
void update(int a)
{e[a].max=max(e[LS(a)].max,e[RS(a)].max),e[a].sum=e[LS(a)].sum+e[RS(a)].sum;}
void build(int l,int r,int a)
{
e[a].l=l,e[a].r=r;
if(l==r){e[a].sum=e[a].max=w[l];return;}
build(l,(l+r)>>1,LS(a)),build(((l+r)>>1)+1,r,RS(a)),update(a);
}
void change(int x,int k,int a)
{
if(e[a].l==x&&e[a].r==x){e[a].sum=e[a].max=k;return;}
if(x<=((e[a].l+e[a].r)>>1))change(x,k,LS(a));
else change(x,k,RS(a));
update(a);
}
int query_sum(int l,int r,int a)
{
if(l<=e[a].l&&e[a].r<=r)return e[a].sum;
int tot=0;
if(l<=((e[a].l+e[a].r)>>1))tot+=query_sum(l,r,LS(a));
if(r>((e[a].l+e[a].r)>>1))tot+=query_sum(l,r,RS(a));
return tot;
}
int query_max(int l,int r,int a)
{
if(l<=e[a].l&&e[a].r<=r)return e[a].max;
int tot=INT_MIN;
if(l<=((e[a].l+e[a].r)>>1))tot=max(tot,query_max(l,r,LS(a)));
if(r>((e[a].l+e[a].r)>>1))tot=max(tot,query_max(l,r,RS(a)));
return tot;
}
void init1(int u)
{
siz[u]=1,dep[u]=dep[fa[u]]+1;
for(int i=0;i<g[u].size();i++)
if(g[u][i]!=fa[u])fa[g[u][i]]=u,init1(g[u][i]),siz[u]+=siz[g[u][i]];
}
void init2(int u)
{
int nxt=0,maxn=0;pos[u]=cnt++;
for(int i=0;i<g[u].size();i++)
if(g[u][i]!=fa[u]&&siz[g[u][i]]>maxn)nxt=g[u][i],maxn=siz[g[u][i]];
if(!nxt)return;
top[nxt]=top[u],init2(nxt);
for(int i=0;i<g[u].size();i++)
if(g[u][i]!=fa[u]&&g[u][i]!=nxt)
top[g[u][i]]=g[u][i],init2(g[u][i]);
}
int query(int a,int b,bool f)
{
int tot=f?0:INT_MIN;
while(top[a]!=top[b])
{
if(dep[top[a]]>dep[top[b]])swap(a,b);
if(f)tot+=query_sum(pos[top[b]],pos[b],1);
else tot=max(tot,query_max(pos[top[b]],pos[b],1));
b=fa[top[b]];
}
if(pos[a]>pos[b])swap(a,b);
if(f)tot+=query_sum(pos[a],pos[b],1);
else tot=max(tot,query_max(pos[a],pos[b],1));
return tot;
}
int main()
{
scanf("%d",&n);
for(int i=1,a,b;i<n;i++)
scanf("%d%d",&a,&b),g[a].push_back(b),g[b].push_back(a);
init1(1),top[1]=1,init2(1);
for(int i=1;i<=n;i++)scanf("%d",&w[pos[i]]);
build(0,cnt-1,1),scanf("%d",&q);
for(int i=1,a,b;i<=q;i++)
{
scanf("%s%d%d",opt,&a,&b);
if(!strcmp(opt,"CHANGE"))change(pos[a],b,1);
else if(!strcmp(opt,"QMAX"))printf("%d\n",query(a,b,0));
else printf("%d\n",query(a,b,1));
}
return 0;
}
3 条评论
TPLY · 2018年1月15日 7:40 下午
ztO (ABS)&&(XZY) Orz
konnyakuxzy · 2018年1月15日 8:19 下午
OrzLTP 赶紧膜 Orz
这种树链剖分您早就学会了吧 QvQ
Orz 太强了
就不要 J 型 D 蒟蒻惹 QvQ
话说 boshiDalao 正在翻译英文题目 Orz
我都没资格翻译啊 QvQ
TPLY · 2018年1月15日 8:36 下午
刚刚开始学树剖 emm
说了我很弱啦
刚刚才 A 的树的统计 (我弱死了)
TPLY · 2018年1月15日 8:41 下午
有没有常数小点的板子, 我的书剖常数大得要死
konnyakuxzy · 2018年1月15日 9:17 下午
啊?
我觉得我的板子挺好啊
好像没被卡过诶 QvQ
害怕.jpg
boshi · 2018年1月15日 9:19 下午
树剖主要是线段树的常数要小。查询修改反之和倍增没啥两样,常数可以忽略 (前提是你不做无用的查询)。所以你需要学常数小的线段树
boshi · 2017年6月30日 3:31 下午
你觉得找重儿子是不是在 init1() 里方便一些。就可以少几个循环。
boshi · 2017年6月29日 10:00 下午
膜膜膜太强了
konnyakuxzy · 2017年6月29日 10:06 下午
哈哈哈你发的没我快= ̄ω ̄=
<(= ̄ˇ ̄=)>