什么是后缀数组?
假设我们现在有一个字符串”ababa”
我们知道这个数组有一些后缀,分别是(以下后缀 i 指以 i 为开头的后缀)
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| ababa | baba | aba | ba | a |
现在我们按照字典序将它们排序,得到:5 3 1 4 2,那么我们令 $SA_1=5,SA_2=3,SA_3=1…$便得到了后缀数组 SA
如何求后缀数组?
给一道例题:洛谷 P3809
主要思想是倍增,可以结合图,文字说明和代码进行查看。
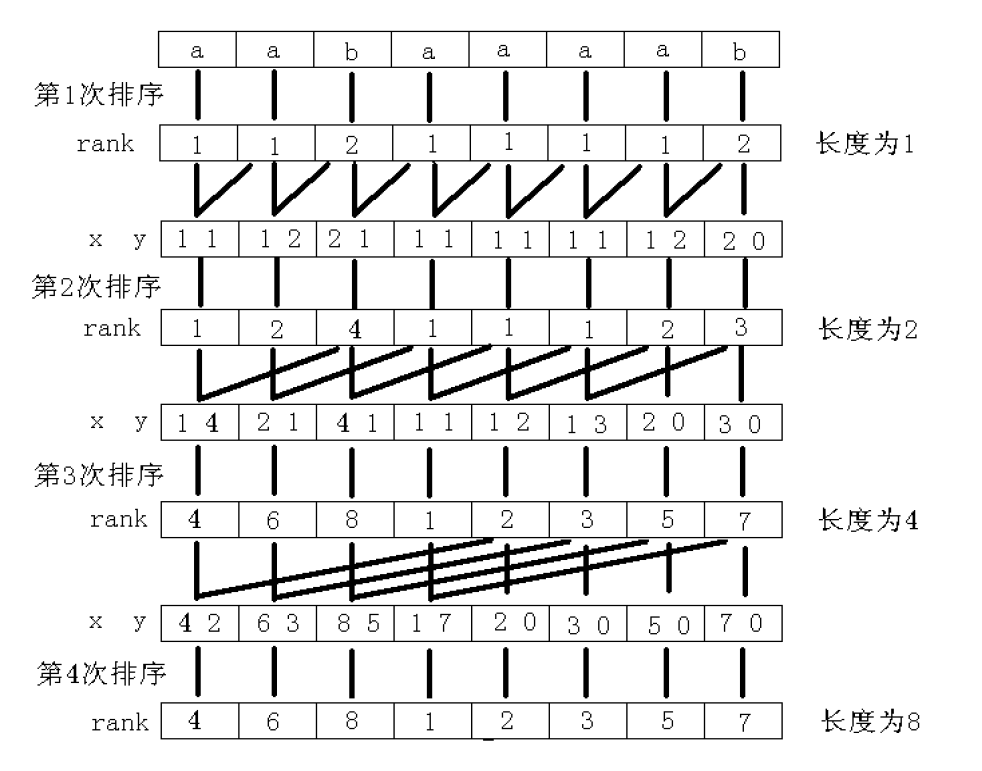
假设现在我们已经排序完成了所有长度为 num 的子串,并得到了当前子串们的 SA(排完序后的顺序)和 $x_i$(又称 rank,即以 i 开头的子串的排名)
现在我们的任务是排序所有长度为 num+num 的子串,那么,我们令一个这样的子串由两个长度为 num 的子串 A 和 B 组成。现在,我们的任务是以 A 为第一关键字,B 为第二关键字进行基数排序。
定义 $y_i$:第二关键字排名为 i 的子串开头的位置,以下步骤是求出 $y_i$:
1. 对于末尾溢出的子串,它们的第二关键字为 0,对它们进行处理。
2. 对于所有长度为 num 的子串,如果它们的开头大于 num,则可以作为一个长度为 num+num 的子串的第二关键字,然后根据它们的 SA 来求一些 $y_i$
km=0;
for(int i=n-num+1;i<=n;++i) y[++km]=i;
for(int i=1;i<=n;++i) if(SA[i]>num) y[++km]=SA[i]-num;
然后,求出新的 SA 值。
1. 开一个桶 T,将每个关键字 2 对应的关键字 1 塞进桶里。
2. 利用每个关键字 2 对应的关键字 1 的排名,更新 SA(即基数排序)
void Rsort() {
for(int i=0;i<=m;++i) T[i]=0;
for(int i=1;i<=n;++i) ++T[x[y[i]]];//y: 关键字 2-> 子串开头,x: 子串开头-> 关键字 1
for(int i=1;i<=m;++i) T[i]+=T[i-1];
for(int i=n;i>=1;--i) SA[T[x[y[i]]]--]=y[i];
//从后往前。因为关键字 2 已经排序了,而每次-1, 是从大到小确定排名为 T[x[y[i]]] 的子串开头
}
最后,求出新的 $x_i$。这个只要利用 SA 就行了,同时还要利用上一次的 $x_i$,用于对比两个子串是否相同,进行去重。
由于子串长度溢出末尾就补 0 这个操作,所以最后一次我们排序的 n 个子串一定是所有后缀了。
完整代码实现就是:
#include<bits/stdc++.h>
using namespace std;
const int N=1000005;
char s[N];
int n,m,a[N],SA[N],x[N],y[N],T[N];
void Rsort() {
for(int i=0;i<=m;++i) T[i]=0;
for(int i=1;i<=n;++i) ++T[x[y[i]]];
for(int i=1;i<=m;++i) T[i]+=T[i-1];
for(int i=n;i>=1;--i) SA[T[x[y[i]]]--]=y[i];
}
int cmp(int i,int j,int num) {return y[i]==y[j]&&y[i+num]==y[j+num];}
void getSA() {
for(int i=1;i<=n;++i) x[i]=a[i],y[i]=i;
m=127,Rsort();//m: 当前有多少种排名
for(int km=1,num=1;km<n;num+=num,m=km) {//如果当前生成的排名数量有 n 个以上,那么排完了
km=0;
for(int i=n-num+1;i<=n;++i) y[++km]=i;
for(int i=1;i<=n;++i) if(SA[i]>num) y[++km]=SA[i]-num;
Rsort(),swap(x,y),x[SA[1]]=km=1;//用 y 暂存 x 的值用于比较
for(int i=2;i<=n;++i) x[SA[i]]=cmp(SA[i],SA[i-1],num)?km:++km;
}
}
int main()
{
scanf("%s",s),n=strlen(s);
for(int i=0;i<n;++i) a[i+1]=s[i]-' ';
getSA();for(int i=1;i<=n;++i) printf("%d ",SA[i]);
return 0;
}
后缀的最长前缀
$Height_i$: 排名为 i 和 i-1 的两个后缀的最长公共前缀
$H_i$: 后缀 i 和排名在其前面的后缀的最长公共前缀
我们可以证明一个性质:$H_i \geq H_{i-1}-1$
假设后缀 k 是后缀 i-1 的前一名,最长前缀就是 $H_{i-1}$,去掉一个字符,变成了后缀 k+1 和后缀 i。
如果 $H_{i-1}$等于 0 或 1,$H_i \geq 0$显然成立
否则,k+1 一定是 i 的前一名,则 $H_{i-1} – 1 \leq H_i$
于是我们可以 O(n) 计算 $Height_i$啦!
void getHei() {
int lcp=0;
for(int i=1;i<=n;++i) {
if(lcp) --lcp;
int j=SA[x[i]-1];
while(a[j+lcp]==a[i+lcp]&&lcp<n) ++lcp;
Hei[x[i]]=lcp;
}
}
后缀数组的基本应用
洛谷 P2408:每一个子串必定是一个后缀的前缀。我们把后缀 i 与后缀 i-1 的公共前缀看作是后缀 i 独有的子串,那么答案就是 $\sum_i^n (n-SA_i+1-Height_i)$
bzoj1717/洛谷 P2852:二分答案 ans。如果在 Height 数组中,连续的大于等于 ans 的数大于等于 K-1 个(因为 K-1 个 Height 对应 K 个子串嘛),说明当前答案可行,否则不可行。
bzoj1692/洛谷 P2870:比较从队首与队尾的字母字典序大小,如果一样,就要依次比较。所以干脆将原串翻转过来粘在后面,然后求这个长度为 2n 的新串的后缀数组,依次贪心比较获得答案。
spoj220:把所有的串粘在一起,中间用不同的特殊字符隔开(这样简单方便一些)。二分答案 ans,扫描 Height 数组,提取其中 $Height_i \geq ans$的区间 [l,r],对于所有 i 属于 $[SA_{l-1},SA_r]$,是否其中在每个字符串中最小和最大的之间相差大于等于 ans,如果是,则该答案为合法。
HDU3948: 把字符串改成跑 manacher 要用的形式,然后用 manacher 搞出每一个字符向左和右可以得到的回文长度 p,再求出字符串的 SA 和 Height。然后每个字符造成的贡献是 $(p[SA_i]-min(Height_i,p[SA_{last}]))/2$,这个 last 是指,如果以某个字符为中心的回文串,被完全包括在了上一个字符为中心的回文串中,那么就跳过这个字符,用这种方式得到的上一个字符。
0 条评论