【题解】bzoj1367 sequence 左偏树 ——litble

假设给出数列 a，求一个单调不降的数列 b，要求最小化 $\sum |a _ i -b _ i|$。
如果 a 是单调不减的数列，考虑 b 的构造方式，如图：

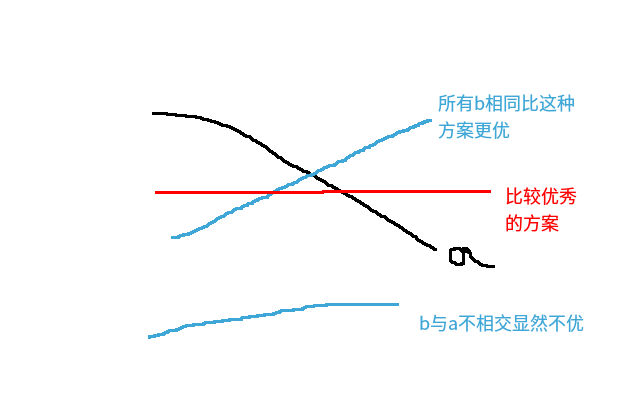
那么所有的 b 要取同一个值。先假定取当前 a 序列的中位数（中位数的定义是将 a 从小到大排序后，第 $\lceil \frac{n}{2} \rceil$个数），发现如果将 b 的那条线向上移动，那么与 a 线的交点就会往左移，也就是说，与 b 线距离增加的点数增加了，与 b 线距离减少的点数减少了。将线往下移同理。所以说此时 b 取中位数最优。
但是现在 a 序列不是单调不增的，我们就把它划分成若干个单调不增的序列，每一个序列取一个 b。现在的问题就是，这些 b 之间不是单调不减的。
考虑两个单调不增序列 $A_1$和 $A_2$，其中 $A_1$的中位数较大，$A_2$的中位数较小。同样画图分析

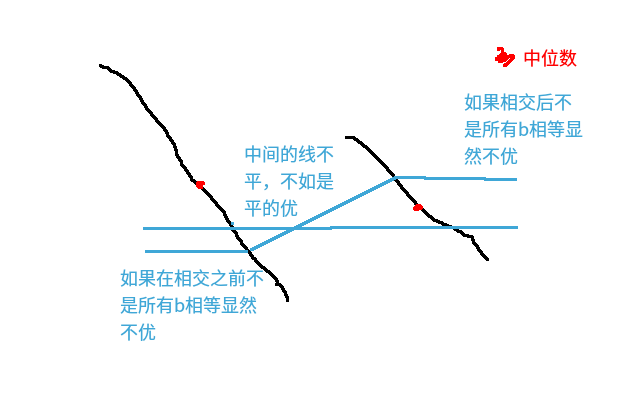
解释一下，中间的线如果不是平的，那么将左边的线往上移，右边的往下移，都可以使得与这个线距离变小的点增加，会产生更优秀的方案。
那么这两个区间合并，找到的所有 b 也一定相同。那么此时可以将这两个区间看作一个处理，我们已经证明过整个区间的 b 都相同时，取中位数最优，所以我们就要取这两个区间的中位数当 b。
那么怎么实现快速合并中位数呢？使用左偏树。每次开个大根堆，当堆中元素数量大于这个堆代表的区间的元素数量的一半时，不断弹出堆顶元素，这样堆顶的元素就是中位数了。合并两个区间相当于合并两个堆。
嗯，最后，我们将这个问题改回求的 b 是单调上升序列，那么我们可以认为我们每次在求一个 $i+b_i$，$b_i$单调不降。也就是将每个 $a_i$减去 $i$，然后其他做法完全相同。

#include<bits/stdc++.h>
using namespace std;
#define RI register int
int read() {
    int q=0;char ch=' ';
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
    return q;
}
typedef long long LL;
const int N=1000005;
int rt[N],sz[N],L[N],R[N],A[N],B[N];
struct node{int ls,rs,d,v;}t[N];
int n,js;LL ans;
int merge(int a,int b) {
    if(!a||!b) return a|b;
    if(t[a].v<t[b].v) swap(a,b);
    t[a].rs=merge(t[a].rs,b);
    if(t[t[a].rs].d>t[t[a].ls].d) swap(t[a].ls,t[a].rs);
    t[a].d=t[t[a].rs].d+1;
    return a;
}
int main()
{
    n=read();
    for(RI i=1;i<=n;++i) {
        A[i]=read()-i;
        ++js,rt[js]=i,sz[js]=1,L[js]=i,R[js]=i,t[i].v=A[i];
        while(js>1&&t[rt[js-1]].v>t[rt[js]].v) {
            sz[js-1]+=sz[js],R[js-1]=R[js];
            rt[js-1]=merge(rt[js-1],rt[js]),--js;
            while(sz[js]>(R[js]-L[js]+2)/2)
                rt[js]=merge(t[rt[js]].ls,t[rt[js]].rs),--sz[js];
        }
    }
    for(RI i=1;i<=js;++i)
        for(RI j=L[i];j<=R[i];++j) B[j]=t[rt[i]].v;
    for(RI i=1;i<=n;++i) ans+=1LL*abs(A[i]-B[i]);
    printf("%lld\n",ans);
    return 0;
}