1. 题目
2. 题解 A: 自适应暴力
这题一开始看的时候并没有像大佬们一样一眼就看出了这个是光的折射。。。
然后就写了个能 AC 的暴力——自适应暴力
首先我们很容易想到直接从起点到终点连一条直线。
并且也很容易想到路径一定是折线。
有这两点就能打暴力了。
暴力怎么打呢?
首先呢,连一条从起点到终点的直线
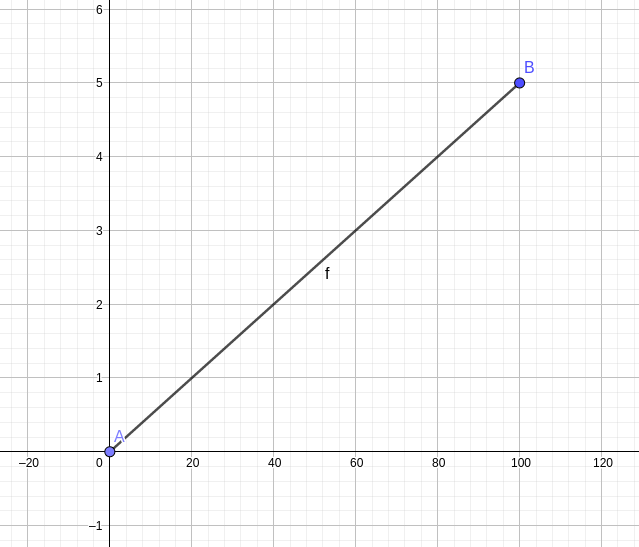
现在我们要通过把这条线段 “折” 起来使得所用时间最少。
“折” 的地方肯定是在此线段与区域交界线的交点处,上下移动该交点就能 “折” 这根线。
我们随机选定一个点,上下移动它,使得它的前驱节点经过它到达它的后继节点所用时间最少
比如:
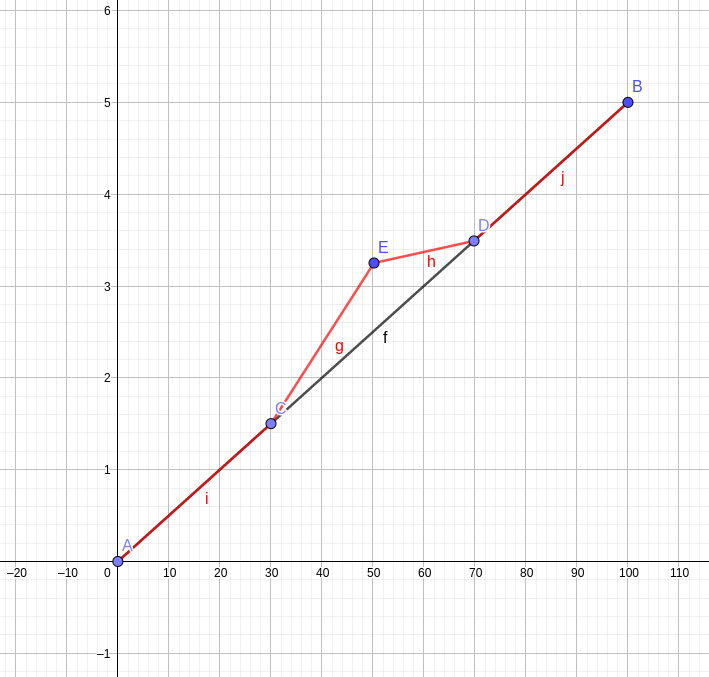
我们随机选中了点 $E$,由于 $x \in [30,50]$区域的通行速度比较大,而 $x \in [50,70]$区域的通行速度比较小,所以把点 $E$上移可以使得点 $C$通过点 $E$到点 $D$的时间变短。
我们找到最优的一个移动方法移动点 $E$即可。
这种情况下,$C$到 $D$的花费时间关于点 $E$的高度呈一个单峰函数(有唯一极值),用三分法即可在 $log$的复杂度内求出点 $E$的新坐标。
这样子的新坐标是否是最优的呢?
显然不是
上图所示的情况中,我们移动了点 $E$以后,可能导致点 $A$通过点 $C$到达点 $E$的时间不是最小的,需要判断点 $C$的新的最优位置,进行移动。。。
移动了点 $C$以后又可能要移动点 $A$。。。以此类推。。。
(当然点 $D$也可能需要移动,但是我们最好不要移动它,因为移动它可能会导致来回修改点 $E$、点 $D$的位置,复杂度很高,还不如等以后随机到点 $D$的后面的点的位置来更新它)
这样一条路走到底,就会把整个路径更新一遍,路径也就更靠近最优路径了。
然后如果更新途中,某次更新大小不超过 $eps$,就不向下递归更新了,这样节省复杂度。
随机次数需要玄学调参,23333~
当然不管怎么说这个方法还是很暴力的,最后 9 秒多跑过的 OvO…
代码(注意代码后面还有题解 B =。=):
#include <bits/stdc++.h>
#define NS (105)
#define REG register
#define eps (3e-4)
using namespace std;
int n, C = 450000; // 随机次数
double d[NS], f[NS], Y, fx[NS], ans, tot;
inline double str(REG double x, REG double y) // string,弦长
{
return sqrt(x * x + y * y);
}
inline double fmn(REG int a) // 三分法找函数极值
{
REG double l = fx[a - 1], r = fx[a + 1], mid, fl, fr;
while (r - l > eps * 2)
{
mid = (l + r) * 0.5;
fl = str(d[a], mid - eps - fx[a - 1]) * f[a];
fl += str(d[a + 1], fx[a + 1] - mid + eps) * f[a + 1];
fr = str(d[a], mid + eps - fx[a - 1]) * f[a];
fr += str(d[a + 1], fx[a + 1] - mid - eps) * f[a + 1];
if (fl < fr) r = mid; else l = mid;
}
return (l + r) * 0.5;
}
double tmp;
void fix(REG int a)
{
if (--C <= 0) return;
tmp = fx[a], fx[a] = fmn(a);
if (abs(tmp - fx[a]) > eps && a > 1) fix(a - 1);
}
int main(int argc, char const* argv[])
{
scanf("%d%lf", &n, &Y), srand(n * 233);
for (REG int i = 1; i <= n; i += 1) scanf("%lf", &d[i]), tot += d[i];
for (REG int i = 1; i <= n; i += 1) scanf("%lf", &f[i]), f[i] = 1 / f[i];
for (REG int i = 1; i <= n; i += 1) tmp += d[i], fx[i] = tmp * Y / tot;
while (C > 0 && n > 1) fix(rand() % (n - 1) + 1);
for (REG int i = 1; i <= n; i += 1)
ans += str(d[i], fx[i] - fx[i - 1]) * f[i];
printf("%.3f\n", ans);
return 0;
}
题解 B: 费马光程原理
自然真玄妙
费马光程原理的内容大概就是:
光传播的路径是光程取极值的路径
那么根据折射定律:
$$\frac {sin \alpha} {V _ \alpha} = \frac {sin \beta} {V _ \beta}$$
其中 $sin \alpha$和 $sin \beta$表示光线与法线夹角,$V _ \alpha, V _ \beta$分别表示光线在介质 $\alpha,\beta$中的传递速率。
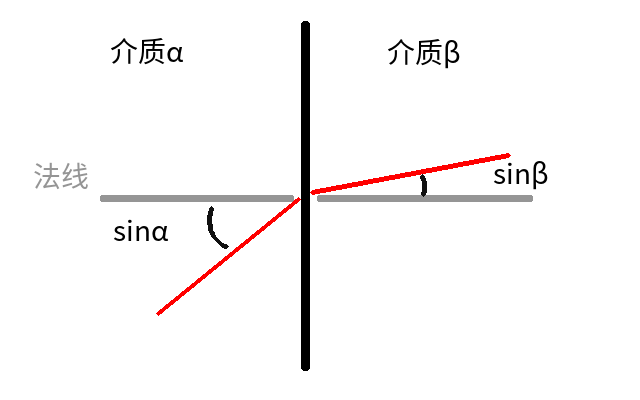
由此,我们确定了第一个入射角,后面的入射角就都确定了。
因此二分第一个与法线的夹角的 $sin$值,找到某个 $sin$值使得最后的光线能刚好打中终点。
这里精度要求非常高,因此我们二分的时候不用 $eps$判断是否二分到答案了,而是暴力进行大概 100 次的二分过程,这样精度不会有丢失。
复杂度就很低了,总共是 $nlog _ 2(\frac {1} {eps})$级别的(然而其实并不是)。
代码:
#include <bits/stdc++.h>
#define NS (105)
using namespace std;
int n;
double X, H[NS], V[NS], ans;
inline double str(double x, double y)
{
return sqrt(x * x + y * y);
}
bool check(double s1)
{
double rem = 0;
for (int i = 1; i <= n; i += 1)
{
rem += H[i] * tan(asin(s1));
s1 = s1 / V[i] * V[i + 1];
}
return rem <= X;
}
int main(int argc, char const* argv[])
{
scanf("%d%lf", &n, &X);
for (int i = 1; i <= n; i += 1) scanf("%lf", &H[i]);
for (int i = 1; i <= n; i += 1) scanf("%lf", &V[i]);
double l = 0, r = X / str(H[1], X), mid;
for (int C = 1; C <= 100; C += 1)
{
mid = (l + r) * 0.5;
if (check(mid)) l = mid;
else r = mid;
}
l = (l + r) * 0.5;
for (int i = 1; i <= n; i += 1)
{
ans += H[i] / cos(asin(l)) / V[i];
l = l / V[i] * V[i + 1];
}
printf("%.3f\n", ans);
return 0;
}
0 条评论