It self
名称:树状数组 (Binary-Indexed-Tree),顾名思义,是一种树形的结构。但他的树形体现在索引上 (Indexed),本体依旧是数组。
性质:树状数组支持以下几种操作:
1. 单点加 (logN) 与区间求和 (logN)
2. 区间加 (logN) 与单点求和 (logN)
3. 区间加 (logN) 与区间求和 (logN)
相比与线段树,它的时间复杂度 (常数)、空间复杂度、编程复杂度都有所降低。唯独不支持无交换率的操作,这也许涉及到群论的相关理论。
Why does it exist
简单来说,树状数组利用二进制位的拆分,将某个位置数值改变量分散存储,查询时再从分散存储的地方取出合并。做到了 logN 级别完成普通数组 N 级别完成的工作。
树状数组的分散存储有赖于 lowbit 函数。即:lowbit(x)=x&-x。该函数可求 x 二进制下最低的一位 1,如 lowbit(10010[2])=00010[2]。
lowbit:我们先思考,如何求一个二进制数最低的一位 1。考虑到这一位后面全部是 0,那我们能不能利用以此运算将后面的 0 全部改变,没有改变的那一位的后一位就是 lowbit(x)?当然可以。但是这样比较复杂,我们不如将这个数按位取反,现在 x=10010,(~x)=01101。我们将 (~x) 加一,它身后的所有 1 变成了 0,最后一位 0 变成了 1。现在我们再将 (~x) 和 x 按位求与,结果就是 lowbit(x) 了。根据计算机补码的特性,我们完全可以写成:lowbit(x)=x&((~x)+1)=x&-x。这就是最简单的 lowbit 函数。
It’s beauty
先来了解一下树状数组的形态,它长这样:
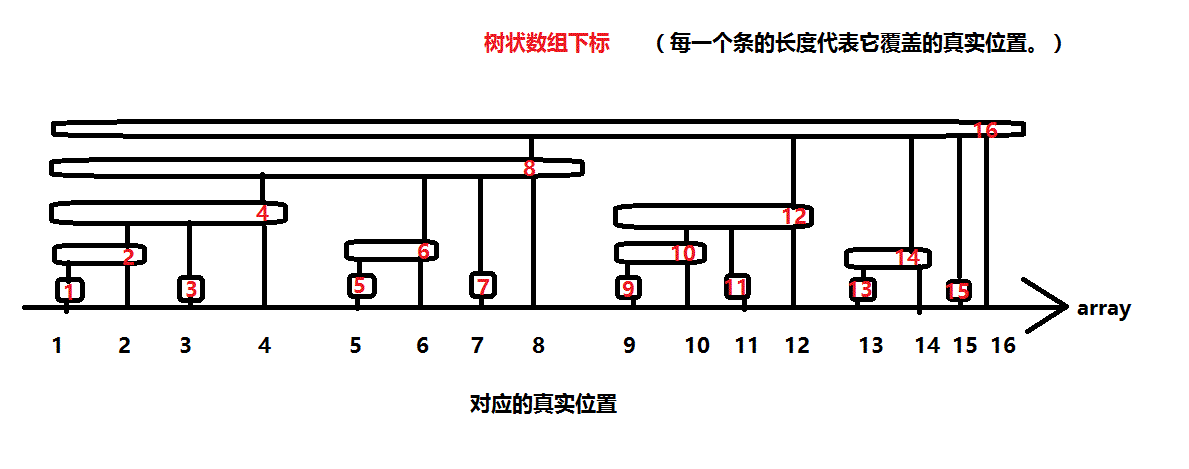
如果我们用它来维护前缀和,每修改一个真实位置,我们把它头顶的每个长条都更改。每次查询前缀和,我们用不重不漏的长条覆盖真实位置。
如果我们用它来维护每个真实位置的值,每次区间修改,我们用长条覆盖从 1 到 pos 的区间。每次查询真实值,我们把它头顶的每个长条的值加起来。
于是,我们就慢慢理解了树状数组的美丽之处。
更注意:长条的高度取决于长条编号的 lowbit 值,高度越高的长条也越长 (长度为二的高度次幂),覆盖的范围也越大。因此我们现在可以引出树状数组的真谛了:
原理:树状数组的每个下标 x, 比如 101000 它的含义其实是:下标为 100xxx 的元素和。也就是说它可以保存下标为 100000,100001,100010… 的真实值的和。同理,如果我们要访问 100101, 我们也应该访问所有包含了它的长条,也就是 100101,10010x,100xxx,xxxxxx。结合 lowbith 函数,我们访问某个位置头顶长条的时候,x 不断加上 lowbit(x) ,访问某个区间时,x 不断减去 lowbit(x)。这就是树状数组可以 logN 操作的原因,也是它与 lowbit 函数紧密相关的原因。
Advanced BIT
我们可以容易想出树状数组只涉及一个区间操作的模式。如果同时区间加和区间求和呢?
先从差分的角度来看前缀和。
如果给某个区间同时加上一个数,那么这个数列的差分值只有 2 个地方改变:序列首和序列尾。而查询一段区间我们需要查询差分值的前缀和。因此我们应该考虑维护差分序列而不是原序列。
设 $d_i=x_i-x_{i-1}$(特别地,x0=0)
$$
x_a=\sum\limits_{i=1}^{a}{d_i}
$$
$$
\sum\limits_{i=1}^{a}{x_i}=\sum\limits_{i=1}^{a}{\sum\limits_{j=1}^{i}{d_i}}=\sum\limits_{i=1}^{a}{(a-i+1)d_i}=(a+1)\sum\limits_{i=1}^{a}{d_i}-\sum\limits_{i=1}^{a}{id_i}
$$
所以我们只需要分别维护 $\sum\limits_{i=1}^{a}{d_i}$和 $\sum\limits_{i=1}^{a}{id_i}$就可以了。
Problem solved by BIT
有了树状数组,我们就可以 A 题啦。以下是一些水题。
线段树练习 3(CodeVS1082)
HH 的项链 (BZOJ1878)
The k-th Largest Group(POJ2985)
Matrix(POJ2155)
Kiki’s k-number(HDU2852)
inversion(高级数据结构 U6)
moofest(高级数据结构 U6)
stars(高级数据结构 U6/HDU1156)
apple(高级数据结构 U6/POJ3321)
orders(高级数据结构 U6)
prime(高级数据结构 U6/UVa11610)
Disharmony Trees(HDU3015)
Ping pong(LA4329)
2 条评论
konnyakuxzy · 2017年8月27日 10:41 上午
%%% 做了这么多题太强啦 Orz%%%%%
【算法】 树状数组 —— by juruo-oier – K-XZY · 2018年8月25日 8:09 下午
[…] 这有神犇 boish 的 树状数组心得 […]