浅析解析式法在一类题目中的运用

拯救 Protoss 的故乡

浙江省绍兴市第一中学的潘宇超在 2010 年的论文中出了这样的一道题:

给定一棵 $n$个点的树，树的每条边有上下界 $[a,b]$，每条边上可以有一个流量 $f$，如果 $f\leq a$，则花费为 0，如果 $a<f\leq b$，则花费为 $f-a$，$f$不能大于 $b$。求根节点到所有叶子节点的一个最大的流，使得总花费不超过 $m$

其中 $n\leq 10^5,m\leq10^6$

原题正解

出题人给出的做法是一种优化后的费用流。该做法在本文中不做讨论。

另一种解法

性质 1：

不难发现这样一个性质：最小费用 $y$关于总流量 $x$的函数是一个下凸的函数。其原理大致是，每当流量增加，必然会有更多的边达到 $(a,b]$区间内。

这个性质对于原树和它的任意一棵子树都成立。

将费用函数化

我们不妨将最小费用 $y$与总流量 $x$的关系函数化。由于这是一个离散函数，我们可以很方便的用一次函数完美逼近这个函数。为了方便，我们可以维护一次函数的斜率，即原函数的导数。

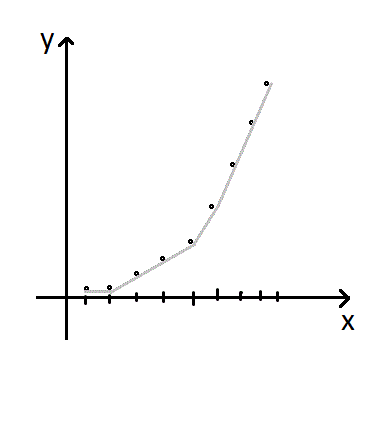
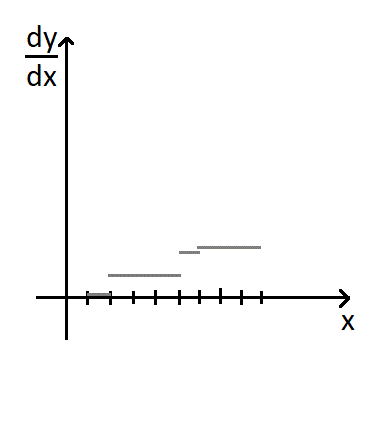
由于原函数值域在 $[0,m]$范围内的取值才是我们关心的，所以 $f(x)$超过 $m$后的部分我们可以忽略掉。下面我们将证明忽略这些部分后对于任意形态的函数，我们只需要 $O(\sqrt{m})$的空间即可表示。

对于一段一次函数，我们可以用 $O(1)$的空间表示，那么最多有几段一次函数呢？最坏情况下，每一段一次函数覆盖 $x$轴的长度均为 $1$，那么 $t$段函数后 $y$的最小值将是 $y=\sum_{i=1}^ti=\frac{t(t+1)}{2}$，又因为 $y\leq m$，所以 $t\leq O(\sqrt{m})$，也就是说最坏情况下一个函数我们只需要 $O{\sqrt{m}}$的空间。

函数的合并

接下来，我们会想利用这些函数 Dp。对于流向节点 $a$的流量，我们需要尽可能优的分配到各个子树中，使总价值最小。感性理解一下，由于价值随流量递增，且流量最小元为 1，所以对于每个大小为 1 的流量，我们贪心地将它分配到接受它后花费变化更小的子树中，可以证明这样一定是最优的。所以，我们接下来需要将这个 Dp 过程也函数化。

接受它后花费变化最小，即函数的导数最小，意思就是我们每次将所有子树中斜率最小的一次函数接到当前节点的一次函数后面即可。这个的代价是 $O(k\sqrt{m})$的，其中 $k$是子节点个数，故合并函数的总时间复杂度为 $O(n\sqrt{m})$。

函数的更新

对于流向一个节点的流量，产生花费的地方不止是子树中的边，还有流向这个节点的边。

所以，我们还需要根据流向某个节点的边的特征，更改该节点的函数值。

具体要支持的操作有：

截取：将 $x$超过最大流的部分截断
累加：将 $x$属于 $(a,b]$部分的函数斜率加一。(即导函数加一)。

这两个操作的目的是显而易见的，其具体实现也非常简单，这里不再赘述，两个操作都可以在 $O(\sqrt{m})$的时间内完成。

时间复杂度

函数的单次合并、更新复杂度为 $O(\sqrt{m})$，故总时间复杂度为 $O(n\sqrt{m})$，可以轻松通过本题。

空间复杂度

由于每个节点最多需要 $O(\sqrt{m})$的空间，所以总共需要 $O(n\sqrt{m})$的空间。这是我们难以承受的。

但是，如果结合动态内存分配，需要的总空间将会非常少。在原题的数据中使用了不到 55MB 的空间。

下面对于几种特殊形态的树，给出 dfs 时动态分配内存后的峰值空间复杂度 (仅考虑函数部分)。

链：$O(\sqrt{m})$
完全二叉树：$O(log{n}\sqrt{m})$
菊花树：$O(\sqrt{m})$
竹子：$O(n\sqrt{m}log^{-1}m)$

可以证明，再找不到比竹子更坑爹的树了，于是本题的空间复杂度可以定为：$O(n\sqrt{m}log^{-1}m)$

代码实现

下面的代码维护的是原函数的导数。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#define MX 200005

using namespace std;

typedef long long ll;

struct func
{
    ll *x,*k;int n;
    void init()
    {
        n=2;
        x=new ll[4];
        k=new ll[4];
        x[1]=1000000,x[2]=1000000;
        k[1]=1000000,k[2]=1000000;
    }
    void comb(const func& a,const func& b,const ll& mxf)
    {
        static ll tx[2002],tk[2002];
        ll pa=1,pb=1,sum=0,tot=0,now=0;
        tx[0]=tk[0]=0;
        while(pa<=a.n||pb<=b.n)
        {
            if(pa<=a.n&&pb>b.n)
            {
                now++;
                tx[now]=a.x[pa];
                tk[now]=a.k[pa];
                pa++;
            }
            else if(pa>a.n&&pb<=b.n)
            {
                now++;
                tx[now]=b.x[pb];
                tk[now]=b.k[pb];
                pb++;
            }
            else if(pa<=a.n&&pb<=b.n&&a.k[pa]<b.k[pb])
            {
                now++;
                tx[now]=a.x[pa];
                tk[now]=a.k[pa];
                pa++;
            }
            else if(pa<=a.n&&pb<=b.n&&a.k[pa]>b.k[pb])
            {
                now++;
                tx[now]=b.x[pb];
                tk[now]=b.k[pb];
                pb++;
            }
            else if(pa<=a.n&&pb<=b.n&&a.k[pa]==b.k[pb])
            {
                now++;
                tx[now]=a.x[pa]+b.x[pb];
                tk[now]=a.k[pa];
                pa++,pb++;
            }
            tot+=tx[now]*tk[now];
            sum+=tx[now];
            if(sum>=mxf)break;
            if(tot>=1000000)break;
        }
        if(sum>mxf)tx[now]-=(sum-mxf);
        x=new ll[now+2];
        k=new ll[now+2];
        n=now;
        memmove(x,tx,sizeof(ll)*(now+2));
        memmove(k,tk,sizeof(ll)*(now+2));
    }
};

int n,m;
int fst[MX],nxt[MX],v[MX],lm[MX],lx[MX],lnum;

void addeg(int nu,int nv,int nm,int nx)
{
    nxt[++lnum]=fst[nu];
    fst[nu]=lnum;
    v[lnum]=nv;
    lm[lnum]=nm;
    lx[lnum]=nx;
}

void input()
{
    int a,b,c,d;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d%d",&a,&b,&c,&d);
        addeg(a,b,c,d);
        addeg(b,a,c,d);
    }
}

func f[MX];
void dfs(int x,int fa,ll mnf,ll mxf)
{
    int flg=0;
    f[x].init();
    for(int i=fst[x];i;i=nxt[i])
    {
        int y=v[i];
        if(y!=fa)
        {
            flg=1;
            dfs(y,x,lm[i],lx[i]);
            f[x].comb(f[y],f[x],mxf);
        }
    }
    if(!flg)
    {
        f[x].k[1]=0,f[x].x[1]=mnf;
        if(mxf-mnf)f[x].k[2]=0,f[x].x[2]=mxf-mnf;
    }

    ll sum=0;
    for(int i=1;i<=f[x].n;i++)          //函数的 “累加” 操作
    {
        if(sum<=mnf&&sum+f[x].x[i]>mnf)
        {
            if(sum==mnf)
            {
                for(int j=i;j<=f[x].n;j++)f[x].k[j]++;
            }
            else
            {
                f[x].n++;
                ll rlen=f[x].x[i]-(mnf-sum);
                f[x].x[i]=mnf-sum;
                for(int j=f[x].n;j>i;j--)f[x].x[j]=f[x].x[j-1],f[x].k[j]=f[x].k[j-1];
                f[x].x[i+1]=rlen;
                for(int j=i+1;j<=f[x].n;j++)f[x].k[j]++;
            }
            break;
        }
        else sum+=f[x].x[i];
    }
    sum=0;
    for(int i=1;i<=f[x].n;i++)          //函数的 “截取” 操作
    {
        if(sum<=mxf&&sum+f[x].x[i]>mxf)
        {
            if(sum==mxf)f[x].n=i-1;
            else
            {
                f[x].n=i;
                f[x].x[i]=(mxf-sum);
            }
            break;
        }
    }
}

int main()
{
    input();
    dfs(0,-1,1000001000000,1000001000000);
    ll cost=0,used=0;
    for(int i=1;i<=f[0].n;i++)
    {
        if(cost+f[0].x[i]*f[0].k[i]>m)
        {
            used+=(m-cost)/f[0].k[i];
            break;
        }
        else used+=f[0].x[i],cost+=f[0].x[i]*f[0].k[i];
    }
    printf("%lld\n",used);
    return 0;
}

【算法】浅析解析式法在一类题目中的运用 -boshi

于2018年6月30日2018年6月30日由boshi发布